Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 3.3 - Ex. 23
Graduação em enfermagem
A tabela a seguir mostra o número de homens e mulheres matriculados em enfermagem no Centro de Saúde da Universidade de Oklahoma em um semestre recente. Um estudante é selecionado aleatoriamente. Encontre a probabilidade de cada evento. (Adaptado de: University of Oklahoma Health Sciences Center Office of Institutional Research.)
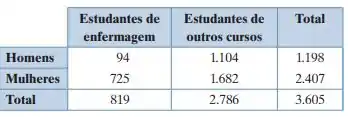
(a) O estudante é homem ou estuda enfermagem.
(b) O estudante é mulher ou não estuda enfermagem.
(c) O estudante não é mulher ou estuda enfermagem.
Passo 1
Salve, fera! Tudo bem? Vamos encarar essa questão! Ela é bem simples.
(a) Analisando a tabela, temos que, a probabilidade do estudante selecionado ser homem ou estudar enfermagem vai ser:
A = Probabilidade de ser homem:
B = Probabilidade de ser estudante de enfermagem:
Probabilidade de A e B acontecer:
Assim, a probabilidade de A ou B acontecer é dada por:
(b) Analisando a tabela, temos que, a probabilidade do estudante selecionado ser mulher ou não estudar enfermagem vai ser:
A = Probabilidade de ser mulher:
B = Probabilidade de ser não estudante de enfermagem:
Probabilidade de A e B acontecer:
Assim, a probabilidade de A ou B acontecer é dada por:
(c) Analisando a tabela, temos que, a probabilidade do estudante selecionado não ser mulher ou estudar enfermagem vai ser:
A = Probabilidade de não ser mulher, ou seja, ser homem. De (a), temos 0,332
B = Probabilidade de ser estudante de enfermagem. De (a), temos 0,227
Probabilidade de A e B acontecer, também de (a), temos 0,026
Assim, a probabilidade de A ou B acontecer é dada por:
Espero ter ajudado! Abraços e até a próxima!
Resposta
(a) 0,533
(b) 0,975
(c) 0,533