Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 9.Problemas - Ex. 36
Houve uma denúncia por parte dos operários de uma indústria de que, toda vez que ocorria um acidente em uma seção da indústria, ocorriam outros em outras seções mais ou menos no mesmo horário. Em outras palavras, os acidentes não estavam ocorrendo ao acaso. Para verificar essa hipótese, foi feita uma contagem do número de acidentes por hora durante um certo número de dias (24 horas por dia). Os resultados da pesquisa foram apresentados no quadro a seguir.
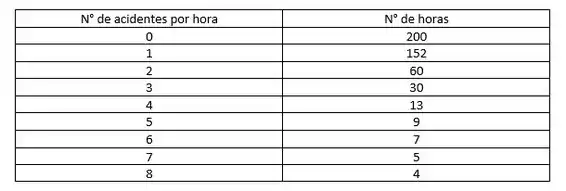
(a) Calcule o número médio de acidentes por hora nessa amostra.
(b) Se o número de acidentes por hora seguisse uma distribuição de Poisson, com média igual à que você calculou, qual seria o número esperado de dias com 0, 1, 2,... etc. acidentes?
(c) Os dados revelam que a suspeita dos operários é verdadeira?
Passo 1
Bom, galerinha. Vamos saber o que precisamos para resolver cada alternativa, beleza?
Na alternativa (a) usaremos a seguinte fórmula para calcular o número médio de acidentes por hora
Na (b) e (c) temos que saber um conceito chamado teste de aderência.
Bom, a ideia de se realizar um teste de aderência é testar se o modelo probabilístico se adequa aos seus dados. Pera, o que?
Aqui no Responde aí, vocês encontraram uma explicação completa e rapidinha sobre teste de aderência.😊
Partiu?
Passo 2
Sendo o número de acidentes,
Passo 3
A tabela a seguir traz o número esperado de horas com 0, 1, 2, ... acidentes, obtido sob o modelo de Poisson, calculados por
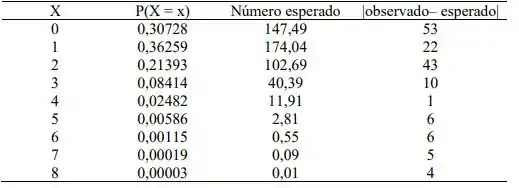
Passo 4
Se for analisada a medida , haverá indicação de que a distribuição não se aproxima de uma Poisson.
Resposta
(a)
(b)
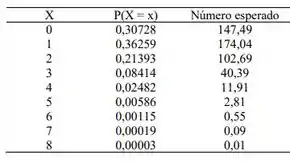
(c) A suspeita dos operários é falsa.