Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 10.Exercícios propostos - Ex. 16
Num inquérito com os telespectadores de televisão de uma cidade, 60 de 200 homens desaprovam certo programa, acontecendo o mesmo com 75 de 300 mulheres. Ao nível de 10%, há uma diferença real entre as opiniões de homens e mulheres?
Passo 1
Olá galerinha, vamos resolver este exercício de acordo com o passo a passo dos testes de hipóteses.
Então primeiramente iremos definir nossa hipótese nula () e alternativa ():
- ;
- .
Queremos testar essa hipótese para . Além disso sabemos que nosso teste é bilateral e como queremos testar a proporção iremos utilizar a variável normal padronizada ():
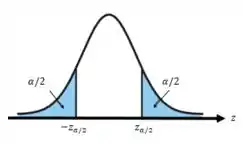
Para este teste temos a seguinte equação:
Onde é a média ponderada das proporções amostrais:
Passo 2
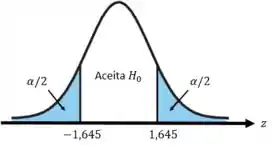
Então pela tabela da distribuição normal conseguimos definir a nossa região crítica:
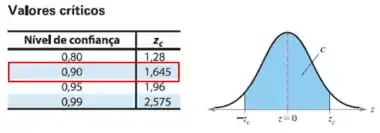
- Se aceita ;
- Se rejeita .
Passo 3
Do enunciado temos:
- ;
- ;
- ;
- .
Então temos as seguintes proporções amostrais ( e ):
E a média ponderada dessas proporções:
Então conseguimos calcular o valor de para compararmos com o crítico ():
Como , então aceitamos e concluímos que ao nível de 10%, não há diferença entre as opiniões de homens e mulheres.
Tchau pessoal, até mais!
Resposta
aceita .