Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 4.Problemas - Ex. 28
Lançam-se, simultaneamente, uma moeda de um real e uma de um quarto de dólar. Em cada tentativa anotou-se o resultado, cujos dados estão resumidos na tabela abaixo.
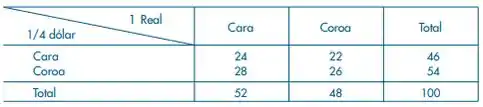
(a) Esses dados sugerem que os resultados da moeda de um real e as de um quarto de dólar estão associados?
(b) Atribua para ocorrência cara o valor 0 e para a ocorrência de coroa o valor 1. Chamando de X1 o resultado do real e de X2 o resultado do quarto de dólar, calcule a correlação entre X1 e X2 . Essa medida está de acordo com a resposta que você deu anteriormente?
Passo 1
(a) Esses dados sugerem que os resultados da moeda de um real e as de um quarto de dólar estão associados?
Primeiro, vamos montar uma tabelinha com os valores observados e esperados?
Com base nesses valores, vamos encontrar uma medida quantificadora de dependência entre as variáveis, ou seja, o .
Se a hipótese de não-associação for verdadeira, o valor calculado de deve estar próximo de zero. Se as variáveis forem associadas, o valor de χ2 deve ser grande 😉.
- Cálculo das frequências esperadas
Vejamos a tabela a seguir. Entre parênteses, encontram-se os valores esperados.
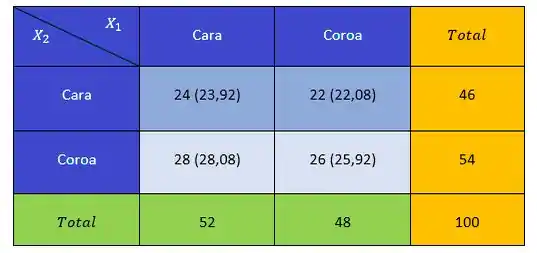
Calculando o qui-quadrado:
Como é pequeno, logo, não há associação entre os resultados das moedas de um real e de um quarto de dólar.
Passo 2
(b) Atribua para ocorrência cara o valor 0 e para a ocorrência de coroa o valor 1. Chamando de X1 o resultado do real e de X2 o resultado do quarto de dólar, calcule a correlação entre X1 e X2 . Essa medida está de acordo com a resposta que você deu anteriormente?
O coeficiente de correlação linear entre as variáveis X1 e X2 é 0, pois X1 e X2 são INDEPENDENTES.
Portanto, NÃO existe correlação linear entre e .
Logo, esse resultado está de acordo com o resultado do item anterior.
Resposta
(a) Não há associação entre os resultados das moedas de um real e de um quarto de dólar.
(b) O coeficiente de correlação linear entre as variáveis X1 e X2 é 0, pois X1 e X2 são independentes. Esse resultado está de acordo com o resultado do item anterior.