Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 38

Para a marca de referência do Conselho de desempenho do processamento da transação do exercício. 10, sejam X, Y e Z e o número médio de operações que seleciona, atualiza e insere requerido para cada tipo de transação, respectivamente. Calcule o seguinte:

covariância entre X e Y.

Correlação entre X e Y.

Covariância entre X e Z.

Correlação entre X e Z.

Passo 1

Primeiro, observe que X, Y e Z denotam o número médio de seleções, atualizações e inserções, respectivamente, que são variáveis aleatórias discretas. Usando a tabela na página 179, as distribuições de probabilidade conjunta para cada combinação de duas variáveis é dada e nós precisamos apenas do seguinte:

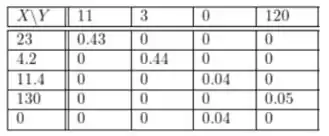
para variáveis aleatórias X e Y, e

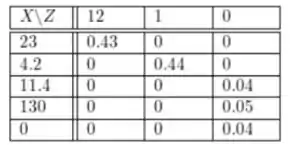
para variáveis aleatórias X e Z.

A partir das tabelas acima, as distribuições marginais para variáveis aleatórias X, Y e Z são dados com:

Passo 2

Calculamos as distribuições marginais por definição:

Pela definição, por exemplo:

Observe que na verdade é a soma da quarta coluna. Temos outras probabilidades para a variável aleatória Y somando as probabilidades em colunas. O mesmo obtemos com as probabilidades para Z, mas olhando para a segunda tabela. Para obter as probabilidades para X somamos as probabilidades em linhas. Nota: não some o valores na primeira coluna e linha, apenas as probabilidades.

A definição da covariância entre as variáveis aleatórias X e Y é

A fim de calcular a covariância entre X e Y, precisamos calcular , de modo semelhante, para calcular a covariância entre X e Z, também precisamos de e . A expectativa matemática da variável aleatória discreta X é a soma do produto de cada possibilidade x com sua probabilidade , então o seguinte é válido:

Para calcular , observe que é uma variável aleatória discreta e que pode ser escrito como , nós sabemos que:

Passo 3

Da tabela de distribuição conjunta temos:

onde as outras partes não foram incluídas porque as probabilidades são 0, então todo o produto é 0. Da mesma forma, temos:

Agora temos tudo para calcular a covariância mas antes de fazermos, vamos ver o que

precisamos para correlação.

A correlação entre as variáveis aleatórias X e Y é definida como:

onde é a variância da variável aleatória X definida como:

A única coisa que falta calcular é . Como sabemos as distribuições de X, Y e Z, as distribuições de são o seguinte:

Acontece que para cada variável aleatória discreta, só precisamos elevar ao quadrado os valores ou e deixe as probabilidades iguais. As expectativas e variações são: