Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 8.Exercícios - Ex. 33
A resistincia do concreto a compressão está scndo testada por um engenheiro civil. Ele testa 12 corpos-de -prova e obtém os scguintes dados.
- Verifique a suposição de que a resistencia a compressão normahnente distribuída. Inclua um gráfico na sua resposta.
- Construa um intervalo de que a resistência à compressão é normalmente distribuída. Inclua um gráfico na sua resposta.
- Construa um limite unilateral inferior de centianca de 95% para a resiste'ncia media. Compare esse limite inferior com o limite inferior do intervalo bilateral de cenfianca c discuta por que são diferentes.
Passo 1
Vamos lá pessoal, se liga aqui como que resolve essa questão:
Letra a:
Crie um gráfico de probabilidade normal.
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com ;
A menor pontuação padronizada corresponde ao menor valor de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
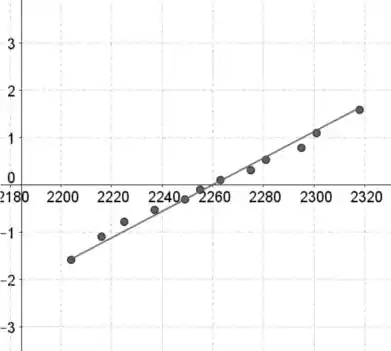
O gráfico de probabilidade normal não contém curvatura forte e o padrão é aproximadamente linear, então podemos concluir que os valores dos dados são aproximadamente normalmente distribuídos.
Passo 2
Letra b
A média é a soma de todos os valores dividida pelo número de valores:
n é o número de valores no conjunto de dados.
A variação é a soma dos desvios de quadráticos da média dividida por n - 1. O desvio padrão é a raiz quadrada da variância:
Determine o valor de t olhando na linha começando com graus de liberdade e na coluna com na tabela V:
O intervalo de confiança é:
Preenchendo os valores conhecidos:
Simplificando:
Passo 3
Letra c:
A média é a soma de todos os valores dividida pelo número de valores:
n é o número de valores no conjunto de dados.
A variação é a soma dos desvios de quadráticos da média dividida por n - 1. O desvio padrão é a raiz quadrada da variância:
Determine o valor de t olhando na linha começando com graus de liberdade e na coluna com na tabela V:
O intervalo de confiança é:
Preenchendo os valores conhecidos:
Simplificando:
Resposta
- Aproximadamente distribuído normalmente