Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.3 - Ex. 66
Média aparada. Para encontrar a média aparada a 10% de um conjunto de dados, ordene os dados, exclua os 10% menores e os 10% maiores valores e determine a média dos valores restantes.
(a) Determine a média aparada a 10% para os dados do Exercício 65.
(b) Compare as quatro medidas da tendência central, incluindo a amplitude média.
(c) Qual é o benefício de se usar uma média aparada versus uma média usando todos os valores dos dados? Explique seu raciocínio.
Passo 1
Valores do exercício 65:
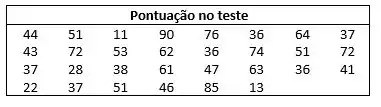
(a) Para encontrar a média aparada a 10% de um conjunto de dados:
Ordene os dados e exclua os 10% menores e os 10% maiores valores:
Novos valores:
Determine a média dos valores restantes. Para o cálculo da média, utilizamos a seguinte equação:
Onde:
valores dados
número de elementos do conjunto de dados
Temos que:
(média aparada a 10% do conjunto)
Passo 2
Item (b):
Para o cálculo da mediana, iremos construir o ROL em ordem crescente:
Temos , um número par, portanto para obter o valor da mediana () devemos fazer uma média aritmética dos dois números centrais.
A moda é o valor que aparece com maior frequência:
A amplitude média é calculada pela seguinte equação:
Resposta
(a)
(b) , e
(c) O benefício de usar a média aparada é o uso de menos valores na hora do cálculo, e comparando os valores encontradas no item (a) e (b) com os valores do exercício 65 (; ; e ), pode-se observar que os valores de média, mediana e moda não se alteraram e a amplitude média teve um valor muito próximo.