Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 10.Exercícios propostos - Ex. 9c

Medidos os diâmetros de 32 peças de uma produção, resultou a distribuição abaixo (valores em mm):

Pergunta-se se há evidência que:

  1. A proporção de peças com diâmetro inferior a 56,9 seja maior que 30%, ao nível de 8%.

Passo 1

Olá galerinha, tudo bem com vocês? Vem comigo!

Vamos resolver este exercício de acordo com o passo a passo dos testes de hipóteses. Então primeiramente iremos definir nossa hipótese nula ( H 0 ) e alternativa ( H a ):

  • H 0 :   p = 0 , 3 0 ;
  • H a :   p ≠ 0 , 3 0 .

Queremos testar essa hipótese para α = 0,0 8 . Além disso sabemos que nosso teste é bilateral e como n > 30 ( n = 32 ), iremos utilizar a variável z . Então a nossa região crítica é definida pelo esquema:

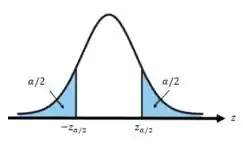
Para este teste temos a seguinte equação:

z = f - p 0 p 0 ∙ ( 1 - p 0 ) n

Onde:

  • f frequência relativo do evento na amostra;
  • p 0 valor da hipótese nula ( p 0 = 0 , 3 0 );
  • n tamanho da amostra ( n = 32 ).

Passo 2

Então pela tabela da distribuição normal conseguimos definir a nossa região crítica:

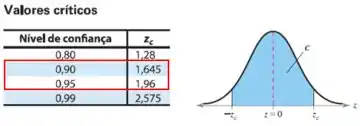
Como não temos o nível de confiança de 0,92, iremos realizar uma interpolação:

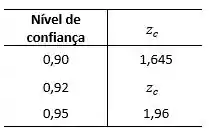
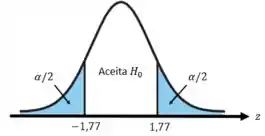
Então temos:

z c - 1 , 645 1,96 - 1 , 645 = 0,92 - 0 , 90 0 , 95 - 0,90

z c = 1 , 77

  • Se - 1 , 77 < z < 1 , 77 aceita H 0 ;
  • Se z > 1 , 77 rejeita H 0 .

Passo 3

Então por último, conseguimos calcular o valor de z e comparar com nossa região crítica. Queremos descobrir a proporção para diâmetro inferior a 56,9, então os valores menores que este:

f = 1 + 3 + 2 + 4 32 = 0 , 3125

Logo:

z = 0,3 125 - 0 , 3 0 0 , 3 0 ∙ ( 1 - 0 , 3 0 ) 32 = 0,15

Como - 1,77 < z < 1,7 7 , então aceitamos H 0 .

Tchau pessoal!

Resposta

z = 0,15 aceita H 0 .

Exercícios de Livros Relacionados

Dois medicamentos para tratamento de infecções bucais estão sendo estudados e o melhor desempenho é definido pela rapizes em eliminar a infecção. Pacientes escolhidos ao acaso receberam um dos medicam
Extraíram-se 25 eixos da produção de cada uma de duas máquinas, e mediu-se a deflexão provocada por uma certa solicitação, tendo sido obtidos os seguintes resultados: ∑ X 1 = 203.10 - 4 m m ∑ X 2 = 45
Uma amostra com 25 elementos, provinda de uma população normal, apresentou média amostral 81. Uma outra com 36 elementos apresentou média 76. Sendo os desvios padrões populacionais de 5,2e3,4 , respec
Dois tipos de soluções químicas A e B foram ensaiadas para se determinar os pH. Observando-se n A = 6 , obteve-se média 7,52 e com n B = 5 obteve-se média 7,49 . Sendo os desvios padrões populacionais
Obtém-se amostras de tamanho três de cada uma de três populações normais, com os seguintes resultados: 3, 5, 4; 11, 10, 12; 16, 21, 17. Testar a hipótese de que as médias populacionais são as mesmas;