Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.2 - Ex. 6
Dois medicamentos para tratamento de infecções bucais estão sendo estudados e o melhor desempenho é definido pela rapizes em eliminar a infecção. Pacientes escolhidos ao acaso receberam um dos medicamentos e tiveram a sua cura classificada em rápida ou não. Deseja-se testar, ao nível de , se os medicamentos são equivalentes. Os dados obtidos são apresentados a seguir.
Qual seria a sua conclusão? Indique as hipóteses do teste e as suposições necessárias.
Passo 1
Fala Clóviss... esse exercício é um bocado diferente do que vínhamos fazendo até o presente momento... trata-se agora, não de um teste de médias, mas sim de um teste de proporção.
Temos o seguinte:
E
Para realizar o teste, supondo uma amostra suficientemente grande, iremos utilizar a seguinte aproximação pela Normal padrão:
Onde,
OBS: vale ressaltar que usamos essa aproximação porque na nossa hipótese nula teremos , se estivéssemos testando com iriamos utilizar outra aproximação. A diferença entre ambas é sútil, mas pode ser decisiva na hora de decidir aceitar ou não a hipótese nula.
Por desencargo de consciência vou citar a aproximação que deve ser usada quando :
Passo 2
Bem tranquilo, vamo definir agora nossas hipóteses:
Beleza, antes do teste vamos descobrir sobre a nossa região crítica, utilizando :
Ou seja, temos de buscar na tabela de distribuição normal um dado tal que:
Mas, se você recordar, a tabela só irá nos fornecer o valor de:
Onde:
Portanto teremos que buscar no corpo da tabela:
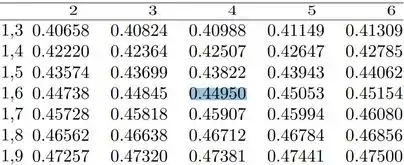
Encontramos o seguinte:
Portanto nossa RC:
Passo 3
Last but not least, precisamos realizar o teste sob :
Portanto, como pertence a região crítica, devemos REJEITAR a hipótese nula.
Resposta
Concluimos então, que existem evidências de que a proporção de pacientes que foram rapidamente curados é diferente para cada medicamento.