Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 10.Exercícios propostos - Ex. 8
As condições de mortalidade de uma região são tais que a proporção de nascidos que sobrevivem até 60 anos é de 60%. Testar essa hipótese, ao nível de 5%, sabendo-se que, em 1.000 nascimentos amostrados, verificaram-se 530 sobreviventes até 60 anos.
Passo 1
Olá galerinha, vamos resolver este exercício de acordo com o passo a passo dos testes de hipóteses.
Então primeiramente iremos definir nossa hipótese nula () e alternativa ():
- ;
- .
Queremos testar essa hipótese para . Além disso sabemos que nosso teste é bilateral e como (), iremos utilizar a variável . Então a nossa região crítica é definida pelo esquema:
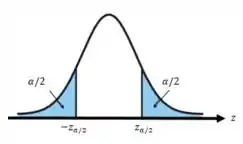
Para este teste temos a seguinte equação:
Onde:
- frequência relativo do evento na amostra;
- valor da hipótese nula ();
- tamanho da amostra ().
Passo 2
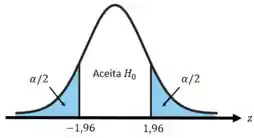
Então pela tabela da distribuição normal conseguimos definir a nossa região crítica:
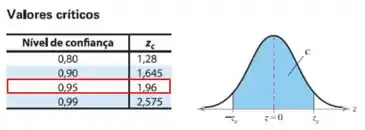
- Se aceita ;
- Se rejeita .
Passo 3
Então por último, conseguimos calcular o valor de e comparar com nossa região crítica. Do enunciado sabemos que:
Logo:
Como , então rejeitamos .
Até mais pessoal!
Resposta
rejeita .