Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 19
Observou-se a produção mensal de uma indústria durante vários anos, verificando-se
que ela obedecia a uma distribuição normal, com variância 300. Foi adotada uma nova
técnica de produção e, durante 24 meses, observou-se a produção mensal. Após esse
período, constatou-se que = 10.000 e = 400. Há razões para se acreditar que a
variância mudou, ao nível de 20%?
Passo 1
Do enunciado, temos:
X = produção mensal
Nova Técnica produção => N=24 meses, = 10.000 e = 400.
Devemos realizar o teste de hipótese para a variância de uma população com distribuição normal.
Temos o seguinte: (qui-quadrado, com n-1 graus de liberdade).
Passo 2
Teste de Hipótese:
Vamos construir a Região crítica: RC={
Onde
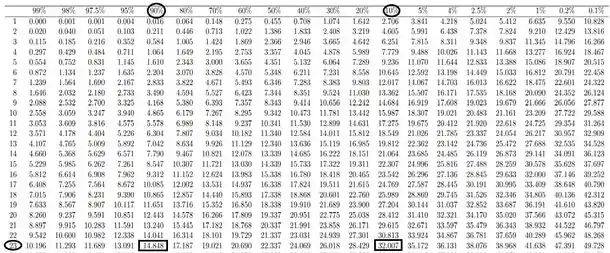
Portanto, RC={}
Passo 3
Teste sob :
Lembrando que o teste sempre é feito sob a hipótese nula, pois ela apresenta igualdade().
Resposta
Portanto, como não pertence a Região Crítica, não rejeitamos e não há evidências de que a nova técnica de produção implementada alterou a variância da produção mensal.