Obtenha ou calcule as seguintes quantidades:
a.
b.
c.
d.
e. O 99º percentil da distribuição F com 1 10, 2 12 f. O 1º percentil da distribuição F com 1 10, 2 12
g. para
h. para ,
Passo 1
Todos os valores podem ser encontrados na tabela A.9 na coluna m-1 e linha n-1.
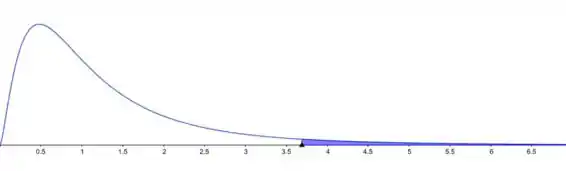
- Neste caso m-1=5, e n-1=8. A área sombreada no gráfico é .
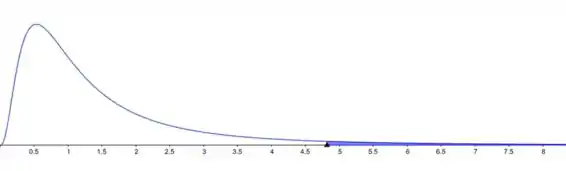
- Neste caso m-1=8, e n-1=5. A área sombreada no gráfico é α=0.05.
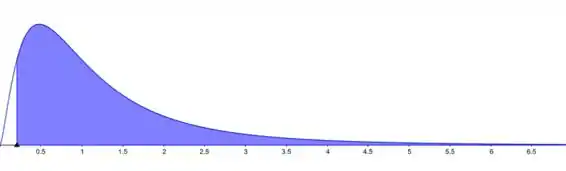
- Neste caso m-1=5, e n-1=8. A área sombreada no gráfico é α=0.95.
- Neste caso m-1=8, e n-1=5. A área sombreada no gráfico é α=0.95.
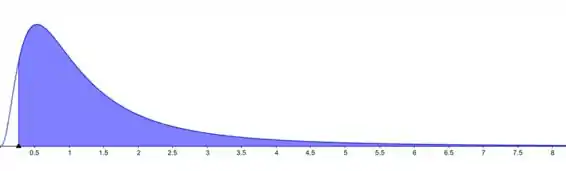
- O 99º percentil da distribuição F com graus de liberdade m-1=10, e n-1=12 é o valor . A área sombreada no gráfico é
- 1º percentil da distribuição F com graus de liberdade , e é o valor . A área sombreada no gráfico é α=0.99
- Seja m-1=6, e n-1=4. Da tabela A.9 no apêndice do livro
- O seguinte vale
Passo 2
Passo 3
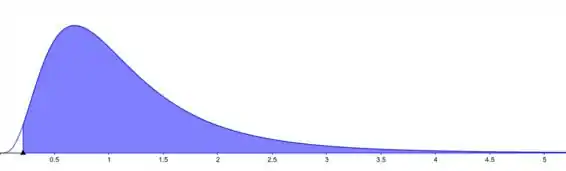
o que implica que
A área sombreada no gráfico representa é .
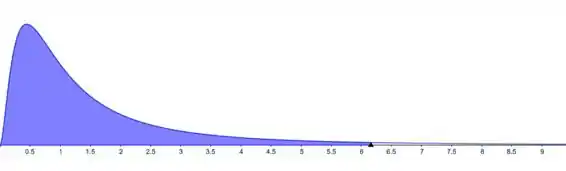
Da tabela
E
Usando isso, é fácil ver (também a partir do gráfico) que
Assim, vale o seguinte
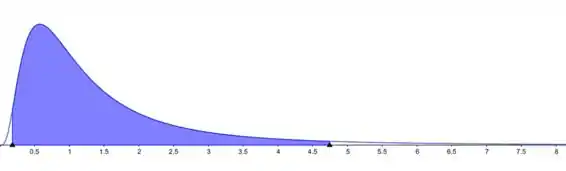
Resposta
- 3.69
- 4.28
- 0.207
- 0.271
- 4.
- 0.212
- 0.95
- 0.94