Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios Suplementares - Ex. 92
Seja X1, ..., Xm, uma amostra aleatória de uma distribuição de Poisson com parâmetro 1 e por Y1, ..., Yn uma amostra aleatória de outra distribuição de Poisson com parâmetro 2. Desejamos testar H0: 1 2 0 contra uma das três alternativas-padrão. Uma vez que para uma distribuição de Poisson, quando m e n são grandes, pode ser usado o teste z de amostra grande da Seção 9.1. Entretanto, o fato de V(X) /n sugere que um denominador diferente deve ser usado na padronização de X Y. Desenvolva um procedimento de teste de amostra grande apropriado para este problema e aplique-o aos dados a seguir para testar se as densidades de mudas de uma determinada espécie são iguais em duas regiões diferentes (onde cada observação é o número de mudas encontradas em um quadrante de amostragem quadrada localizado aleatoriamente com área de 1 m2 ; assim, para a região l, existem 40 quadrantes em que uma muda foi observada etc.):
Passo 1
Proposição: Para uma variável aleatória X com Distribuição de Poisson com parâmetro , o seguinte é verdadeiro
Como mencionado,
O desvio padrão para pode ser calculado como
Para formar uma estatística de teste, o desvio padrão precisa ser estimado. Primeira estimativa e , como de costume, com
Passo 2
Isso produz estatística de teste com distribuição normal padrão (para m e n grandes)
A tabela a seguir resume os dados para realizar este teste
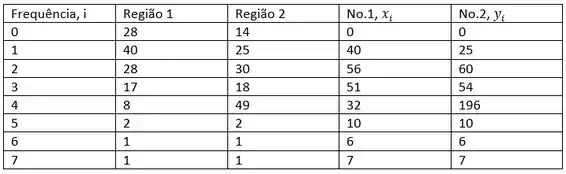
A média amostral para o número de plantas na região 1 é
e para a região é
O valor da estatística z é
Dependendo da hipótese alternativa, o valor de P seria diferente. A hipótese alternativa de interesse é ; assim o valor de PP é duas vezes a área sob a curva zz à direita do valor |z|
Então rejeitar hipótese nula em qualquer nível de significância razoável. O valor foi calculado usando software (você pode usar a tabela no apêndice.
Resposta
Rejeitar hipótese nula.