Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 5.Problemas - Ex. 13

Obtenha as probabilidades dos eventos que aparecem nos Problemas 7 e 12.

Passo 1

Primeiro, vamos relembrar os espaços amostrais e os eventos que aparecem nos Problemas 7 e 12?

Problema 7

Ω = { C C ,   C R ,   R C ,   R R }

A = ( p e l o   m e n o s   u m a   c a r a ) =   { C C ,   C R ,   R C }

B = d u a s   c a r a s = C C

B c = o   c o m p l e m e n t a r   d e   B = { C R ,   R C ,   R R }

Problema 12

A = { 3,6 ; 4,5 ; 5,4 ; 6,3 }

B = { 4,1 ; 4,2 ; 4,3 ; 4,4 ; 4,5 ; 4,6 ; 5,1 ; 5,2 ; 5,3 ; 5,4 ; 5,5 ; 5,6 ; 6,1 ; 6,2 ;

                        6,3 ; 6,4 ; 6,5 ; ( 6,6 ) }

A ∪ B = { 3,6 ; 4,1 ; 4,2 ; 4,3 ; 4,4 ; 4,5 ; 4,6 ; 5,1 ; 5,2 ; 5,3 ; 5,4 ; 5,5 ; 5,6 ;

                                                6,1 ; 6,2 ; 6,3 ; 6,4 ; 6,5 ; ( 6,6 ) }

A ∩ B = { 4,5 ; 5,4 ; 6,3 }

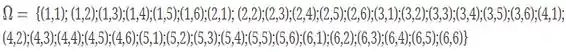
Bora obter as probabilidades?

Passo 2

Problema 7

Temos um total de 4 resultados possíveis, logo

P A = 3 4

P B = 1 4

P B c = 3 4

Passo 3

Problema 12

Temos um total de 36 resultados possíveis, logo

P A = 4 36

P B = 18 36

P A ∪ B = 19 36

P A ∩ B = 3 36

P A c = 32 36

Resposta

Problema 7

P A = 3 4

P B = 1 4

P B c = 3 4

Problema 12

P A = 4 36

P B = 18 36

P A ∪ B = 19 36

P A ∩ B = 3 36

P A c = 32 36

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove as seguintes relações: F = F E ⋃ F E c eE ⋃ F = E ⋃ E c F .
Para qualquer sequência de eventos E 1 , E 2 , … . , defina uma nova sequência F 1 , F 2 , … . , de eventos disjuntos (isto é, eventos tais que F i F j = ∅ sempre que i ≠ j ) de forma que, para todo n
Prove as seguintes relações: F = F E ⋃ F E c eE ⋃ F = E ⋃ E c F .