Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 6.Problemas - Ex. 15
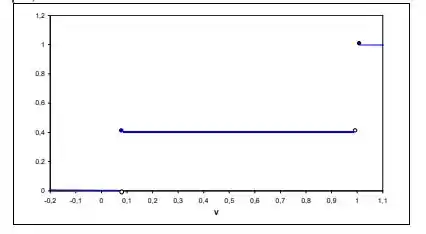
Obter a f.d.a. para a v.a. V do Problema 11. Faça seu gráfico.
Passo 1
Dada a variável aleatória V, chamaremos de função de distribuição acumulada (f.d.a.), ou simplesmente função de distribuição (f.d.) F(v) à função
Sabemos que é igual ao salto que a função dá no ponto .
Então, pela função de probabilidade de V do Problema 11 sabemos que:
Passo 2
Agora vamos montar a f.d.a. de V?
Temos três intervalos certo? Eles são
Para calcularmos a f.d.a. de cada intervalo apresentado precisamos:
1º) Usar a f.p. de V do Problema 11.
2º) Lembrar que estamos falando da distribuição acumulada, portanto sempre precisamos olhar para o intervalo anterior.
Partiu?
Bom, temos apenas dois pontos e o primeiro ponto é 0, portanto antes dele podemos falar que F(v) = 0.
Nesse intervalo a função da um “salto” de 0 para q.
Como o salto foi de (1-q) e estávamos no ponto q, chegaremos no ponto: (1-q) + q = 1.
Escrevendo mais bonitinho...
Passo 3
Observe que o domínio de F é todo o conjunto dos números reais, ao passo que o contradomínio é o intervalo [0,1]. Dessa forma, podemos escolher qualquer número real entre 0 e 1 para fazermos o gráfico. Vamos escolher q = 0,4.
O gráfico da f.d.a de X, F(x) é:
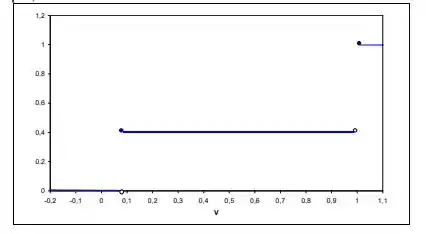
Resposta
