Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 13.Problemas - Ex. 23
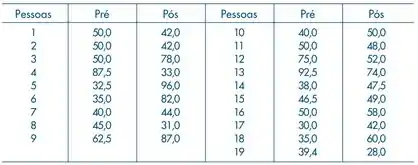
Os dados abaixo referem-se a medidas de determinada variável em 19 pessoas antes e
depois de uma cirurgia. Verifique se as medidas pré e pós-operatórias apresentam a
mesma média. Que suposições você faria para resolver o problema? Faça gráficos apro-
priados para verificar suas suposições.
Passo 1
Como os resultados foram coletados nas mesmas amostras, antes e depois da cirurgia, trata-se de um caso em que as populações não são independentes.
Temos então um caso de duas populações com distribuição normal e PAREADAS:
Onde é a média amostral das n diferenças e é a variância amostral dessas diferenças.
Do enunciado, temos o seguinte:
Obs:
Passo 2
Teste de hipótese:
Construindo Região Critica:
Considerando
Temos:
Lembrando que na tabela de t-student quando temos um limite bilateral:
Nossa região crítica assume a seguinte forma:
Passo 3
Teste sob
Resposta
Portanto como não pertence à região crítica, não rejeitamos , e existem evidencias de que as as médias pré e pós operatório são as mesmas.
Consideramos distribuição normal, com populações pareadas.