Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 13.Problemas - Ex. 20a
Para verificar a importância de um cartaz nas compras de certo produto, procedeu-se do
seguinte modo:
(a) formaram-se sete pares de lojas;
(b) os pares foram formados de modo que tivessem as mesmas características quanto à
localização, ao tamanho e ao volume de vendas;
(c) num dos elementos do par, colocou-se o cartaz; no outro, não;
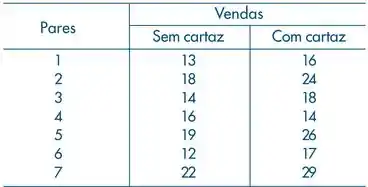
(d) as vendas semanais foram registradas, e os resultados estão a seguir.
Qual seria a sua conclusão sobre a eficiência do cartaz? Use o teste t, fazendo as supo-
sições necessárias.
Passo 1
Primeiramente vamos definir a variável:
Para esse exercício vamos considerar que foram feitas duas medições sobre uma mesma amostra(par); dessa forma, temos que considerar que as duas populações(cada membro do par) normalmente distribuídas e PAREADAS.
Temos portanto, a seguinte aproximação:
Onde é a média amostral das n diferenças e é a variância amostral dessas diferenças.
Do enunciado:
Obs:
Passo 2
Teste de hipótese:
Obs: como fizemos a diferença como sendo () e estamos testando uma possível melhora, nossa hipótese alternativa deve ser unilateral superior(“>”), pois estamos testando ().
Construindo Região Critica:
Considerando
Então:
Lembrando que na tabela de t-student quando temos um limite unilateral superior:
Nossa região crítica assume a seguinte forma:
Passo 3
Teste sob
Resposta
Como , rejeitamos e concluímos que existem evidencias de que o cartaz é eficiente em aumentar as vendas.