Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 2.3 - Ex. 6
Paradois eventos e ,num mesmo espaço amostral, verifique, através de um diagrama, que é sempre possível escrever o evento como sendo e que, portanto, vale
Passo 1
Eaí, tudo bem? Bora resolver esse exercício?
O exercício nos pede para provarmos que , e consequentemente,
Ah, o exercício quer que mostramos essa relação através de um driagrama. Então bora construir?
Passo 2
Observe que: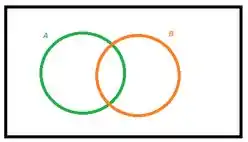
E agora, vamos representar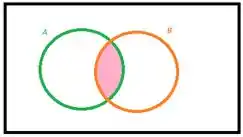 
Representaremos agora, :
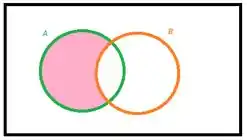
Passo 3
Assim, , e consequentemente,
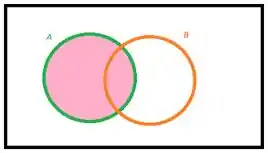
Resposta
Como no enunciado o lote é grande, podemos concluir que sem reposição não alteria significamente as probabilidades.
Exercícios de Livros Relacionados
(h) Um relógio mecânico pode parar a qualquer momento por falha técnica. Mede-se o ângulo (em graus) que o ponteiro dos segundos forma com o eixo imaginário orientado do centro ao número 12.
Três jogadores A, B e C disputam um torneio de tênis. Inicialmente, A joga com B e o vencedor joga com C, e assim por diante. O torneio termina quando um jogador ganha duas vezes em seguida ou quando
(d) Numa entrevista telefônica com 250 assinantes, anota-se se o proprietário tem ou não máquina de secar roupa.
Acredita-se que numa certa população, 20% de seus habitantes sofrem de algum tipo de alergia e são classificados como alérgicos para fins de saúde pública. Sendo alérgico, a probabilidade de ter reaçã
Estatísticas dos últimos anos do departamental estadual de estradas são apresentadas na tabela a seguir, contendo o número de acidentes incluindo vítimas fatais e as condições do principal motorista e