Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 13.Problemas - Ex. 18

Um partido afirma que a porcentagem de votos masculinos a seu favor será 10% a mais que

a de votos femininos. Em uma pesquisa feita entre 400 homens, 170 votariam no partido,

enquanto que entre 625 mulheres, 194 lhe seriam favoráveis. A afirmação do partido é

verdadeira ou não? Caso rejeite a igualdade, dê um IC para a diferença.

Passo 1

X = p o r c e n t a g e m   d e   v o t o s .

Do enunciado temos:

p ^ h = 170 400 = 0,425

p ^ m = 194 625 = 0,3104

Considerando que as populações tenham distribuição normal, sejam independentes e tomando α = 5 % :

Teste de hipótese:   H 0 : p h - p m = ∆ 0 = 0,1   e       H 1 : p h - p m ≠ 0,1

Como ∆ 0 ≠ 0 , devemos utilizar a seguinte aproximação:

Z = p ^ h - p ^ m - ∆ 0 p ^ h 1 - p ^ h n h + p ^ m 1 - p ^ m n m   ~ N ( 0,1 )

Passo 2

Construção da Região Critica: R C = z 0 ∈ R z 0 < - z α 2   o u   z 0 > z α 2

Onde: z 0,025 = ± 1,96

Lembrando que o valor mostrado na tabela, é referente ao p = 0,5 - α 2 = 0,475 , quando o limite é bilateral.

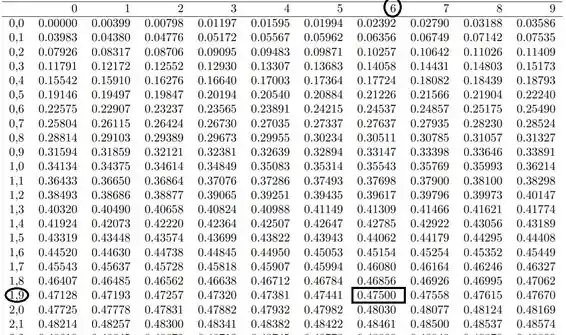
Portanto nossa região crítica assume a seguinte forma: R C = z 0 < - 1,96   o u   z 0 > 1,96

Passo 3

Teste sob H 0 :

z 0 = 0,425 - 0,3104 - 0,1 0,425   .   0,575 400 + 0,3104   .   0,6896 625 = 0,4730

Resposta

Como z 0 = 0,4730   n ã o   p e r t e n c e   à   R C , portanto não rejeitamos H 0 , e existem evidencias de que a diferença de porcentagem de votos entre homens e mulheres é igual a 10%, como afirmou o partido.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se n 1 = 12 , n 2 = 10 , S 1 = 6 , S 2 = 5 , provindas de duas populações normais independentes, testar a hipótese de igualdade das variâncias populacionais, ao nível de 5%.
Numa amostra de 250 elementos verificam-se 24 sucessos e noutra de 100 elementos verificaram-se 15 sucessos. Podemos supor idênticas as probabilidades de sucesso nas duas populações, ao nível de 5%?
Num inquérito com os telespectadores de televisão de uma cidade, 60 de 200 homens desaprovam certo programa, acontecendo o mesmo com 75 de 300 mulheres. Ao nível de 10%, há uma diferença real entre as
Um geneticista está interessado na proporção dehomens e mulheres que tem certo tipo de disfunção sangüínea. Em uma amostra aleatória de cem homens, 31têm a disfunção, enquanto somente 24 de cem mulher
Estabeleça as hipóteses nula e alternativa usadaspara testar as afirmações a seguir e determine onde a região crítica está localizada:(a) No máximo, 20% da próxima colheita de trigo seráexportado para