Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 8.Exercícios - Ex. 78
Uma pepulação normal tem uma média conhecida igual a 50 e uma variancia descenhecida.
- Uma amostra aleatoria de n=16 c sclecienada a partir dessa população, sendo es resultados amostrais iguais a. Quão usuais sao esses resultados? Iste é, qual é a prebabilidade de observar uma media amostral tao grande quanto 52 ( eu maior) sc a média em foco conhecida for realmente 50?
- Uma amostra aleatória de n = 30 é sclecienada a partir dessa pepulacao, onde os resultados amostrais iguais. Quao nao-usuais sao esses resultados?
- Uma amostra alcateria de selecienada a partir dessa pepulacao, sendo os resultados amestrais iguais a. Quae nao-usuais sae esses resultados?
- Compare suas respostas dos itens (a) a (c) e explique por que elas são as mesmas ou são difernetes
Passo 1
Seja seja uma amostra aleatória de uma distribuição normal com média desconhecida e variância desconhecida . A variável aleatória
tem uma distribuição t com n - 1 graus de liberdade.
Uma população normal tem uma média conhecida de e a variância desconhecida (a
razão pela qual usamos estatística t). Sabemos que a média da amostra é
e o desvio padrão da amostra é
Passo 2
Letra a:
Sabemos que o tamanho da amostra é n = 16, então os graus de liberdade são n - 1 = 15. Nós precisamos determinar a probabilidade de observar uma amostra média maior de 52, ou seja
(*): Desigualdade não muda se adicionarmos aos lados esquerdo e direito e divida por
Das equações, temos uma variável aleatória
tem uma distribuição t com 15 graus de liberdade. Do Apêndice Tabela V nós sabemos que a probabilidade
Então
do que a probabilidade de observar uma média de amostra maior que 52 é:
Se quisermos determinar o valor exato da probabilidade , usamos algum programa de sua escolha, e chegamos em:
Passo 3
Letra b:
Sabemos que o tamanho da amostra é n = 30, então os graus de liberdade são n - 1 = 29. Nós precisamos determinar a probabilidade de observar uma amostra média maior de 52, ou seja
Das equações, temos uma variável aleatória
tem uma distribuição t com 15 graus de liberdade. Do Apêndice Tabela V nós sabemos que a probabilidade
Então,
do que a probabilidade de observar uma média de amostra maior que 52 é:
Se quisermos determinar o valor exato da probabilidade , usamos algum programa de sua escolha, e chegamos em:
Passo 4
Letra c:
Sabemos que o tamanho da amostra é n = 100, então os graus de liberdade são n - 1 = 99. Nós precisamos determinar a probabilidade de observar uma amostra média maior de 52, ou seja
Das equações, temos uma variável aleatória
tem uma distribuição t com 99 graus de liberdade.
Na Tabela V do Apêndice, não sabemos a probabilidade da variável aleatória , então usamos o mesmo procedimento da parte a) e obtemos.
Passo 5
Letra d:
Se compararmos suas respostas com as partes (a) - (c), concluímos que se o tamanho da amostra aumenta, a probabilidade de observar uma média amostral maior que 52 fica menor.
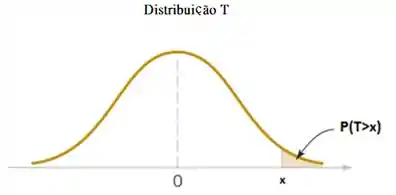
A figura a seguir mostra que para valores maiores de x, a probabilidade é menor. Portanto, se o tamanho da amostra aumenta, os valores
são maiores e a probabilidade de observar uma média amostral maior que 52 é menor.
Resposta
- Ver resolução