Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 9.Exercícios propostos - Ex. 21
Um fabricante de peças acredita que aproximadamente 5% de seus produtos são defeituosos. Se ele deseja estimar a verdadeira porcentagem, dentro de 0,5% de erro, com uma probabilidade de estar certo de 90%, qual o tamanho da amostra a ser tomada?
Passo 1
Olá galerinha, vamos fazer esse exercício juntos? Vem comigo!
Para estimar o valor da proporção (), para verificarmos o tamanho da amostra (), iremos utilizar a seguinte equação:
Do nosso enunciado temos os seguintes dados:
- ;
- ;
- .
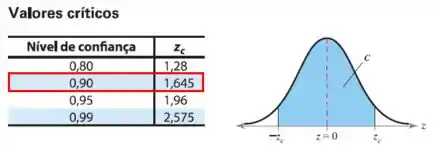
Com o valor de , pela tabela de distribuição normal reduzida, temos o seguinte:
Passo 2
Agora conseguimos encontrar o tamanho da amostra, para estimar a verdadeira porcentagem:
Até mais pessoal!
Resposta
.
Exercícios de Livros Relacionados
Um artigo na revista Journal of sports science apresenta resultados de uma investigação do nível de hemoglobina dos jogadores de hóquei no gelo nas olimpíadas do Canadá. Os dados recortados em (g/dl)
Considere o intervalo de confiança para μ , com desvio padrão conhecido σ : x _ - z α 1 s / n μx _ + z α 2 s / n sendo α 1 + α 2 = α . Seja α = 0.05 e encontre o intervalo para α 1 = α 2 = α / 2 = 0.0
Um experimento clínico foi realizado para determinar se um tipo de vacinação tem efeito sobre certadoença. Uma amostra de 1.000 ratos foi mantida emum ambiente controlado por um período de um anoe 500
Os dados a seguir representam a duração de dois filmes feitos por duas produtoras.Assuma que as diferenças entre as distâncias têm distribuição aproximadamente normal.
Em relação ao Exercício 9.43, determine um intervalo de confiança de 99% para se um pneu de cada marca for atribuído aleatoriamente para cada uma das rodas traseiras de oito táxis e as distâncias, em