Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 9.Exercícios propostos - Ex. 15
De uma distribuição normal com variância 100, retirou-se uma amostra aleatória de tamanho , obtendo-se uma média . Determinar , tal que:
Passo 1
Oi galera, vamos lá!
O valor da probabilidade (), que usualmente assume os valores 90%, 95%, 98%, etc., é denominado nível de confiança e o valor é chamado nível de significância.
Sabemos que a semi-amplitude () do intervalo de confiança da média é dada por:
Supondo que o desvio padrão populacional () é conhecido, e fixando e , podemos determinar através da seguinte equação:
Onde:
Pelo enunciado temos a seguinte equação:
Onde:
- ;
- ;
- .
Passo 2
Para um nível de confiança de 95,4%:
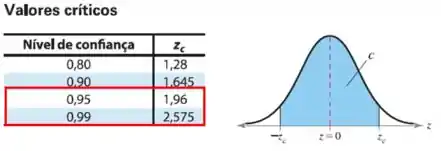
Podemos perceber que não temos o valor de 0,954, então iremos realizar uma interpolação:
Passo 3
Sendo assim, para o nível de confiança de 95,4%:
Tchau galerinha! Te espero em mais exercícios.
Resposta
.