Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 11.Exercícios - Ex. 27
A produção de uma máquina de extrusão contínua de revestimento de tubos de aço com plástico foi investigada como função do perfil de temperatura do termostato ( , em três níveis), do tipo de plástico , em três níveis) e da velocidade do pino giratório que força o plástico por meio de uma matriz de fabricação de tubos ( , em três níveis). Havia duas replicações ( em cada combinação de níveis dos fatores, resultando um total de 54 observações sobre a produção. As somas dos quadrados foram , .
a. Elabore a tabela ANOVA.
b. Use testes apropriados para mostrar que nenhuma das razões para duas ou três interações é significativa ao nível 0,05 .
c. Que efeitos principais parecem significativos?
d. Com , e , use o procedimento de Tukey para identificar diferenças significativas entre os níveis do fator .
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Havia duas replicações ( em cada combinação de níveis dos fatores, resultando um total de 54 observações sobre a produção. As somas dos quadrados foram , .
a. Elabore a tabela ANOVA.
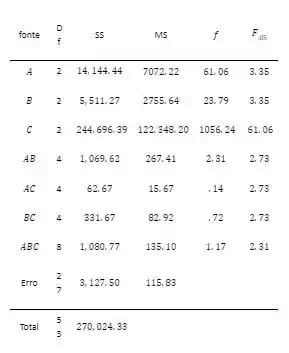
Passo 2
b. As estatísticas f calculadas para todos os quatro termos de interação são menores que os valores tabelados para significância estatística no nível 0,05. Isso indica que nenhuma das interações é estatisticamente significativa.
Passo 3
c. As estatísticas f calculadas para todos os três efeitos principais excedem o valor tabelado para significância no nível 05 . Todos os três efeitos principais são estatisticamente significativos.
Passo 4
d. não é tabelado, use . Todos os três níveis diferem significativamente uns dos outros.
Resposta
a.
b. Isso indica que nenhuma das interações é estatisticamente significativa.
c. Todos os três efeitos principais são estatisticamente significativos.
d. Todos os três níveis diferem significativamente uns dos outros
Espero que tenham aprendido com essa questão, até a próxima !