Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 91
I1-91. Suponha que tenhamos n pares de observações (x,. y,). tais
que o coeficiente de correlação r da amostra seja unitário (aproxi-
madamente).Agora, seja:,= y, e considere o coeficiente de correla-
ção da amostra para os n pares de dados (x.z). Esse coeficiente de
correlação da amostra será aproximadamente unitário? Explique por
que sim. ou por que não.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
A correlação da amostra para o par de variáveis geralmente não será próxima da unidade.
A maneira mais fácil de ver isso é examinar o problema de regressão com as variáveis onde as variáveis assumem valores positivos e negativos. Por exemplo, o gráfico de dispersão para este cenário pode ser parecido com isto:
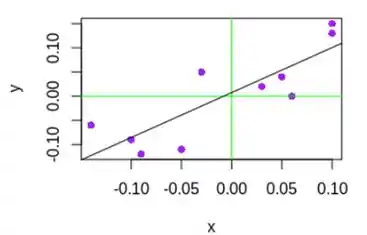
A linha preta é o melhor ajuste linear aos dados. As linhas verdes são eixos coordenados para que você tenha uma melhor impressão dos dados. Você pode imaginar variáveis muito mais fortemente correlacionadas, se quiser.
Passo 2
Agora olhe para o gráfico de dispersão para os dados transformados :
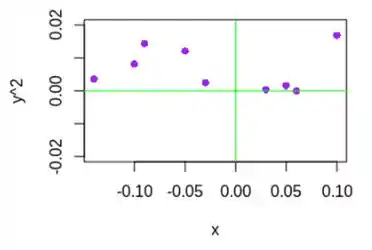
Você pode ver claramente como as variáveis não estão mais linearmente relacionadas, e isso afetaria fortemente o coeficiente de correlação. (ficaria menor).
Resposta
Não.
Pense no que acontece quando você examina duas variáveis x e y com alta correlação, mas com ambas obtendo valores negativos e positivos. Elevar ao quadrado a variável de resposta afeta muito o relacionamento deles!