Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 9.Exercícios - Ex. 50

Os professores consideram seu trabalho gratificante e satisfatório? O artigo "Work-Related Attitudes" (Psychological Reports, 1991, p. 443-450) relata os resultados de uma pesquisa de 395 professores de escola primária e 266 de escola secundária. Dos professores de escola primária, 224 disseram que estavam muito satisfeitos com seus empregos, e dos professores de escola secundária, 126 manifestaram a mesma opinião. Calcule a diferença entre a proporção de todos os professores de escola primária que estão satisfeitos e todos os de escola secundária que também estão satisfeitos, calculando um IC.

Passo 1

Um intervalo de confiança para com nível de confiança de aproximadamente é

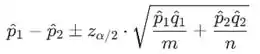
O intervalo de confiança pode ser usado quando e são pelo menos 10. Existem m=395 professores do ensino fundamental e n=266 professores do ensino médio. Há 224 professores do ensino fundamental satisfeitos com seu trabalho,

é a proporção, e 126 professores do ensino médio satisfeitos com seu trabalho,

Passo 2

Portanto, o intervalo de confiança de é

Resposta

Exercícios de Livros Relacionados

Com n 1 = 25 elementos de uma população obtivemos: X - 1 = 8 , S 1 = 1,58 e f 1 = 60 % ; com n 2 = 31 elementos de outra população obtivemos: X - 2 = 7 , S 2 = 1,24 e f 2 = 35 % . Determinar os interv

De uma distribuição normal com variância 100, retirou-se uma amostra aleatória de tamanho n , obtendo-se uma média X - . Determinar n , tal que: P X - - 5 ≤ μ ≤ X - + 5 = 95,4 %

Um fabricante de peças acredita que aproximadamente 5% de seus produtos são defeituosos. Se ele deseja estimar a verdadeira porcentagem, dentro de 0,5% de erro, com uma probabilidade de estar certo de

Numa pesquisa de possuidores de carros numa universidade, entre homens e mulheres, foram obtidos: 24 de 100 homens possuem automóveis e 13 de 100 mulheres possuem automóveis. Determinar, ao nível de 9