Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 9.Problemas - Ex. 46
Prove que E(X) = Var(X) = λ, se a P(X = k) for dada por (6.24).
Passo 1
A fórmula (6.24) é
Ou seja, a questão pede para provarmos que a média e a variância da distribuição de Poisson é λ.
Para isso, precisamos lembrar que a média (ou esperança matemática) e a variância de uma v.a. discreta são dadas por
Passo 2
Provando que ...
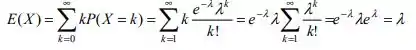
Passo 3
Provando que ...
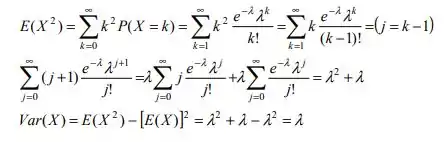
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Em um processo de fabricação que lâmina várias camadas de cerâmica, 1% dos arranjos tem defeitos. Considere que os arranjos seja independente. Qual é o número médio de arranjos que necessitam ser veri
Determine a constante c de modo que a seguinte função seja a função de probabilidade: f ( x ) = c x , para x = 1,2 , 3,4 .
Um fabricante de produtos eletrodomésticos espero que 2% das unidades fale durante processo de garantia. Uma amostra de 500 unidades independentes é rastreada para desempenho de garantia. Qual é a pro
Suspeita-se de que alguns dos reservatórios de produtos químicos comprados de um fornecedor excedam o conteúdo padrão de umidade. Amostras de 30 reservatórios devem ser testados em relação ao teor de
Uma rede congestionada de computadores tem 1% de chance de perder um bloco de dados e perdas de blocos são eventos independentes. Uma mensagem de e-mail requer 100 blocos. Qual é a distribuição de blo