A quantidade de chuva é um fator importante na produtividade agrícola. Para medir esse efeito, foram anotadas, para 8 regiões diferentes produtoras de soja, o índice pluviométrico e a produção do último ano.

1. Faça um gráfico de dispersão e calcule o coeficiente de correlação. Comente o resultado
2. Ajuste a reta de regressão. Como você interpretaria o coeficiente ?
3. Utilizando a reta ajustada no item (c), encontre a produção esperada para uma região com índice pluviométrico igual a 160 mm.
4. É adequado utilizar o modelo ajustado para calcular a produção em uma região cujo índice pluviométrico é igual a 30 mm? Comente.

Gráfico de dispersão:

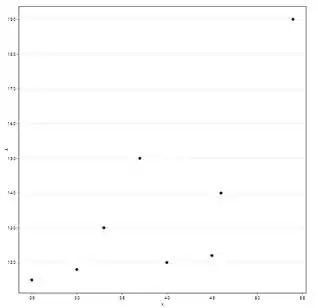
Vamos calcular o coeficiente de correlação de pearson

Lembrando que n=8 (tamanho da amostra)

substituindo os valores e fazendo as continhas:

O coeficiente de relação de Pearson que calculamos anteriormente nos diz que existe uma relação positivo entre a chuva e a produção. Podemos concluir isso pois o coeficiente sendo que quanto mais próxima de -1 e 1, sendo que quanto mais próximo de -1, maior a correlação negativa entre as variáveis, e quanto mais próximo de 1, maior a correlação positiva entre as variáveis.