Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 27
Um estudo foi conduzido para verificar se as pessoas estimam os próprios pesos corretamente. No experimento realizado, 15 pessoas foram selecionadas ao acaso e a cada uma delas perguntou-se os pesos, que depois foram aferidos em balanças devidamente calibradas. Os resultados são apresentados a seguir.
O que pode ser concluído a partir dos dados?
Passo 1
Fala jovem, vamos resolver essa questãozinha aqui...
Olha só, perceba que temos duas amostras pareadas; ainda lembra o que isso significa?
Basicamente, dizemos que as amostras são pareadas, quando realizamos duas medidas na mesma amostra. Perceba que temos dois valores coletados em cima de um mesmo individuo.
Pegou a idéia?? Vamos definir o que estamos estudando:
Podemos realizar o teste utilizando a seguinte aproximação:
Onde é a média das diferenças entre os pesos. Se definirmos o seguinte:
Então podemos ter a seguinte tabela:
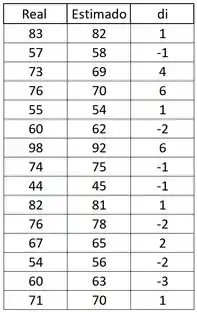
Lembrando que queremos testar o seguinte:
Passo 2
Dessa forma fica mais fácil encontrarmos a média e variância dessas diferenças, lembrando que sempre levamos em consideração os sinais:
E a variância :
Bom, com esses resultados podemos realizar o teste. Mas antes temos que definir nossa região crítica, vamos tomar um nível de significância padrão, :
Ou seja, basta buscar na tabela de t-student um valor tal que:
Mas como você ta manjando muito, já sabe que a tabela só nos dá valores de , e que esse carinha aí é definido assim:
Quando temos uma RC BILATERAL. Lembre-se, caso nossa região crítica fosse UNILATERAL (com sinal de ) teríamos .
Bom, então só precisamos ir na coluna de 5% e na linha de graus de liberdade:
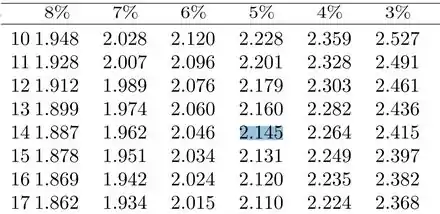
Encontramos que:
Passo 3
Show de bola, agora finalmente podemos realizar o teste sob
Mas em temos , então:
Ou seja, NÃO pertence à região crítica, então devemos ACEITAR a hipótese nula.
Resposta
Com isso, chegamos a conclusão de que as pessoas conseguem sim estimar seus pesos corretamente.