Um experimento com cobaias consistia em comparar o desempenho de uma tarefa para dois métodos de aprendizagem. cada cobaia teve seu desempenho medido, atribuindo-se uma nota de 0 a 10. Essa medição ocorreu imediatamente após cada aprendizagem. Os idealizadores do Método 2 alegam que seu método é mais eficiente e, portanto, deve produzir maior nota. De estudos anteriores, sabe-se que, após uma semana, o aprendizado de um método é esquecido e, portanto, fixou-se esse intervalo de tempo entre a aplicação dos métodos. Além disso, foi estabelecido que o modelo Normal é adequado para as variáveis envolvidas. As notas obtidas foram as seguintes:
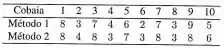
Formule as hipóteses de interesse e faça o teste conveniente, considerando um nível de significância
Passo 1
E ai meu querido, para resolver essa questão temos que fazer um teste de hipótese para testar se houve mudança significativa na poluição sonora em cidades grandes após a campanha educativa:
Vamos seguir o passo a passo do Caso 1 descrito na seção 9.2 do livro. Recomendo que observe a resolução do Exemplo 9.3 porque é similar. Esse exercício também é semelhante com o exercício 1 dessa seção.
Passo 2
Utilizarei uma ferramenta de “Análise de Dados” do Excel, chamada de “Teste-T: duas amostras em par para médias” que vai nos dar o seguinte resultado:
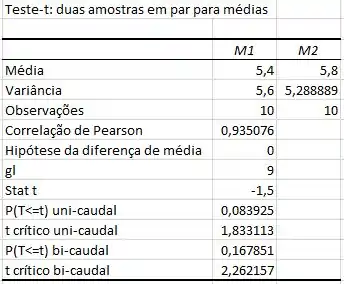
Passo 3
Vamos utilizar a distribuição de t-Student nesse problema e podemos calcular através da seguinte fórmula:
Após esses cálculos o valor encontrado para que é o que o Excel chama de Stat t.
Passo 4
Como estamos tratando de um teste unilateral inferior, temos que nossa região crítica será . Como ele se encontra na região de aceitação e podemos concluir que com um nível de significância de 5% o Método 2 não gera notas maiores que o Método 1.
Resposta
Ei, a resposta está no passo a passo :)