Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 26
Estuda-se a relação linear entre duas variáveis . Uma amostra de 20 pares dessas variáveis forneceu os seguintes valores:
Determine a correlação e ajuste uma reta aos dados.
Passo 1
Mais uma questãozinha de regressão linear; só que dessa vez o autor foi bonzinho demais, ta quase de graça essa.
Bom, tudo que queremos é estimar uma reta do tipo:
Onde e são estimadores para os coeficientes linear e angular respectivamente.
Esses estimadores podem ser obtido assim:
E
E o que queremos testar é se realmente o coeficiente angular é diferente de zero ou não; se ele for diferente de zero então as variáveis estabelecem uma relação linear. Em outras palavras:
Taca-lhe pau nesse carrinho aí então, lembrando que:
e
Com esses dados e os do enunciado, podemos encontrar o coeficiente de correlação:
Crendeuspai...
O lado bom é que temos tudo isso daí, é só substituir:
Lembra que o vai sempre de zero a um, quanto mais próximo de 1 mais “alinhados” são os pontos. Ou seja, o encontrado nos dá a entender que existe sim uma relação linear entre as variáveis.
Para comprovar essa relação, vamos estimar uma reta e realizar a regressão linear.
Passo 2
E então podemos calcular a nossa reta:
E
Temos a seguinte estimação para a reta:
Viu como ta quase de graça?? O enunciado já deu vários dados que vamos precisar para montar a tabela de regressão, que possui a seguinte forma:
Precisaremos calcular as somas dos quadrados:
E
Preciso confessar uma coisa... i lied.
A gente não tem os dados, ponto a ponto para encontrar , a gente teria que substituir cada ponto de e obter até .
Pois é pessoa vamos ter que tirar da cartola. E é da cartola mesmo. Olha só:
Partindo daqui:
Vamos abrir isso:
Mas perceba que não varia com o somatório:
Como não tem nada dentro do último somatório, ele nada mais é do que a soma dos , ou seja:
Guarda essa informação aí com todo amor do mundo (ou não).
E resgata a reta que estamos estimando:
E vamos tacar um somatório ali:
O somatório pode entrar nos parênteses e e não tem nada a ver com isso, então teremos algo assim:
Já temos algo pra voltar naquela fórmula que guardamos a sete chaves no coração.
Agora, seguindo essa mesma ideia, mas antes vamos elevar os dois lados ao quadrado:
E taca-lhe somatório:
E novamente abrindo o produto notável:
Mais uma vez, e não variam com :
Pegou??
É isso, as somas de e o enunciado nos deu. Então se encontrarmos esses podemos obter as somas dos quadrados.
E
Passo 3
Lembra aquela formulazinha que pedi pra você guardar:
Só substituir o que acabamos de achar:
Agora, se você se lembrar de que:
Vai ser mais fácil procurarmos pelo olha só:
Não confunda com o , um seriam os valores amostrais coletados; enquanto o com “chapéu” seriam os obtidos com a reta estimada. E então:
Temos todos os valores, é só substituir:
E como o total é a soma dos do resíduo mais a regressão, para encontrar o resíduo é só subtrair:
Agora, os quadrados médios:
E
E o teste:
Finalmente nossa tabela completinha fica assim:
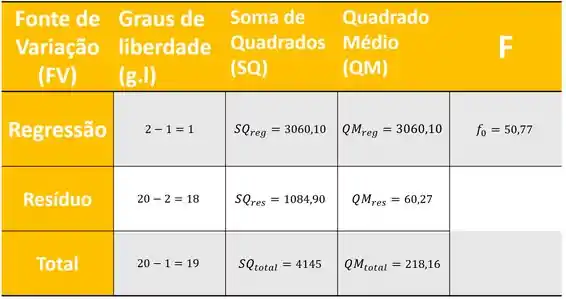
Com certeza você percebeu que é um valor bem grande, mas para avaliar quão grande é esse valor, podemos construir nossa região crítica adotando
Portanto, teremos que buscar na tabela a 5%, um valor tal que:
Para tanto, basta irmos na coluna de 1 grau de liberdade e na linha de 18 graus. Lembrando que você precisa olhar na tabela de 5%.
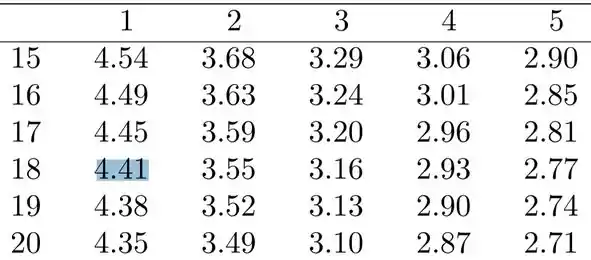
Então nossa região crítica:
E então, temos com muita clareza que pertence a nossa RC e então devemos rejeitar a hipótese nula.
Resposta
Podemos concluir então que realmente as duas variáveis estabelecem uma relação linear entre si.