Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 19c
O custo de manutenção de treminhões movidos a gasolina e a diesel são dados abaixo para duas amostras aleatórias de 10 treminhões de cada tipo. Os veículos considerados trafegam sob as mesmas condições em uma mesma área.
- Teste a igualdade de médias dos dois grupos, considerando .
Passo 1
Odin dai me paciência e foco...
Pois é, ainda falta uma...Mas vamos juntos!
Relembrando que a variável em questão é:
E dessa vez vamos realizar o teste para as médias populacionais; como no item B a gente viu que as variâncias populacionais muito provavelmente são iguais, então aqui teremos que usar a seguinte aproximação:
O que é isso mesmo em??!! Chamamos isso de distribuição t-student com graus de liberdade.
Agora, do que se trata aquele ali?? Ele nada mais é do que uma zueirinha com as variâncias amostrais de cada grupo, olha só:
Outra coisa muito importante, no item B dessa questão a gente encontrou os seguintes valores para as médias e variâncias amostrais de ambos os grupos:
E
Lembra? Vamos deixar engatilhado então o tal do :
Passo 2
Então, agora precisamos usar tudo isso para realizar o seguinte teste:
Vamos começar definindo nossa região crítica, adotando :
O que precisamos fazer é encontrar um determinado valor tal que:
Mas se você se recordar bem, a tabela de distribuição de t-student nos dá, nas colunas, valores ; que são definidos da seguinte forma:
Quando nossa RC for BILATERAL. Lembre-se sempre disso, quando RC bilateral, então ; e quando RC UNILATERAL, .
Então isso significa que deveremos buscar na coluna que representa e na linha de graus de liberdade:
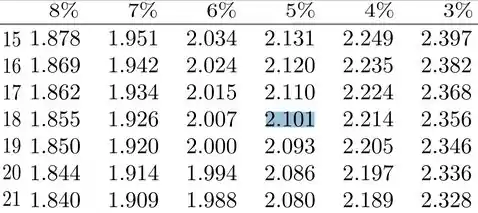
Então encontramos:
Achou a mesma coisa aí??
Passo 3
Só nos resta então realizar definitivamente o teste sob a hipótese nula:
Mas, em temos , portanto:
Ou seja, NÃO pertence a nossa região crítica, então vamos novamente ACEITAR a hipótese nula.
Resposta
Concluindo, evidências mostram que em média os Treminhões movidos a Diesel possuem os mesmos custos de manutenção dos movidos a Gasolina.