Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 31

Reconsidere as quantidades fornecidas no Exercício 18 para a regressão de y fator de deflexão sobre x temperatura. a. Calcule o desvio padrão estimado s ˆ 1 . b. Calcule um IC de 95% para 1, a mudança esperada no fator de deflexão associado com um aumento de temperatura de 1°F.

Passo 1

  1. Vamos determinar S x x ,   S x y   e   S y y

    2. S S R = S x y 2 S x x = - 26.955 2 3662.25 ≈ 0.1984

    T o t a l   S S = S y y = 0.24764

    S S E = T o t a l   S S - S S R = 0.24764 - 0.1984 = 0.04924

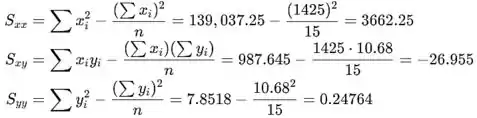
    O desvio padrão do desvio aleatório ϵ é a raiz quadrada da soma dos quadrados do erro dividida por n - 2

    s = S S E n - 2 = 0.04924 15 - 2 ≈ 0.0615

    O desvio padrão da inclinação é o desvio padrão ss do desvio aleatório ϵ dividido pela raiz quadrada S x x .

    s β ^ 1 = s S x x = 0.0615 3662.25 ≈ 0.00102

    Passo 2

  2. c = N i v e l   d e   C o n f i a n ç a = 95 %

Vamos estimar a inclinação da linha de regressão:

Determine o valor t olhando na linha começando com graus de liberdade d f = n - 2 = 15 - 2 = 13 e na coluna com α = ( 1 - c ) / 2 = 0.025 (bicaudal) na tabela da distribuição T de Student:

t α 2 = 2.160

Os limites do intervalo de confiança para β 1 são então

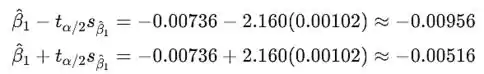
Temos 95% de confiança de que o fator de deflexão associado a um aumento de 1° F na temperatura diminui entre 0.00516 e 0.00956.

Resposta

  1. 0.00102
  2. ( - 0.00956,0.00515 )

Exercícios de Livros Relacionados

A seção de negócios do Washington Times de mar­ço de 1997 listou 21 diferentes impressoras e computadores usados e seus preços de venda. Também listou opreço médio da concorrência. Os resultados parci
Para o modelo de regressão linear simples, proveque Eis2) = a 2
No Exercício 11.49, teste a hipótese de que p = 0contra a alternativa de que p * 0. Use um nível de significância de 0,05.
Considere a regressão da milhagem para certos automóveis, medida em milhas por galão (mpg) em seuspesos em libras (vvt). Os dados são do Consumer Reports(abril de 1997). Parte de um resultado SAS do p
No Exercício 11.30, foi pedido ao estudante quenmostrasse que ^ (yi - j?-) = () para um modelo de rei=lgressão linear simples padrão. O mesmo acontece paraum modelo com intercepto 0? Mostre por que si