Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 33

O Exercício 15 da Seção 12.2 incluiu o resultado do MINITAB para uma regressão da resistência à flexão de vigas de concreto no módulo de elasticidade. a. Use esse resultado para calcular um intervalo de confiança com um nível de confiança de 95% para o coeficiente angular 1 da reta de regressão populacional e interprete o intervalo resultante. b. Suponha que tivéssemos acreditado que, quando o módulo de elasticidade aumenta 1 GPa, a mudança média real associada na resistência à flexão é de no máximo 0,1 MPa. Os dados amostrais contradizem essa afirmação? Expresse e teste as hipóteses relevantes.

Passo 1

Um intervalo de confiança de para a inclinação na linha do modelo de regressão linear simples é

Da saída ; assim, o valor de t é

O intervalo de confiança é (novamente tomando o valor da saída)

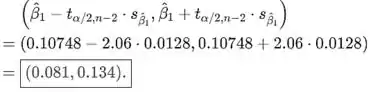
Você pode ter de confiança de que a mudança média real está entre 0.081 MPa e 0.134 MPa

Passo 2

Ao testar contra uma das alternativas, o valor da estatística de teste é

Dependendo da hipótese alternativa, o valor PP pode ser determinado como área correspondente sob . O teste de utilidade do modelo:

No nosso caso, a hipótese nula é

e a hipótese alternativa é

O valor da estatística de teste é

Usando um software ou uma tabela no apêndice, o valor P correspondente é

onde T tem distribuição t-Student com graus de liberdade. Porque

não rejeite a hipótese nula em determinado nível de significância. Não há evidências suficientes de que .

Resposta

Não rejeitar a hipótese nula

Exercícios de Livros Relacionados

Em relação ao Exercício 11.4, use o valor de s2encontrado no Exercício 11.20(a) para calcular(a) um intervalo de confiança de 95% para a média daresistência de corte quando x = 24,5;(b) um intervalo d

Assumindo que ϵ i ' 's sảo normais, independentes e com média 0 e variância comum σ 2 , mostre que A , o estimador dos mínimos quadrados de α em μ Y ∣ x = α + β x , é normalmente distribuído com média

Um professor em uma escola de negócios de uma universidade entrevistou uma dúzia de colegas sobre o número de reunióes profissionais de que eles participaram nos últimos cinco anos ( X ) e o número de

Usando o valor de s2 encontrado no Exercício11.18(a), construa um intervalo de confiança de 95%para no Exercício 11.2.

Para um modelo de regressáo linear simples Y i = α + β x i + ϵ i ,i = 1,2 , … , n , onde ϵ 's sâo independentes e normalmente distribuídos com médias zero e variâncias iguais σ 2 , mostre que Y ˆ e B