Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 34

Consulte o resultado do MINITAB do Exercício 20, no qual x deposição de umidade de x NO 3 e y líquens N(%).

a. Execute o teste de utilidade do modelo no nível 0,01, usando a abordagem da região de rejeição. b. Repita a parte (a), usando a abordagem do valor P. c. Suponha que antes tivéssemos acreditado que, quando a deposição de umidade de NO 3 aumenta em torno de 0,1 g N/m2 , a mudança associada no líquen N esperado é de pelo menos 0,15%. Teste as hipóteses no nível 0,01 para determinar se os dados contradizem esse ponto de vista prévio.

Passo 1

Usaremos o seguinte:

Regressão linear é uma equação linear de duas variáveis ​​das quais uma é independente e uma é dependente da outra. Seja X uma variável independente e Y dependente. A equação linear é definida por:

Y = β 0 + β 1 X

onde β 1 ,   β 1   são coeficientes. E a fórmula para calcular esses coeficientes é a seguinte:

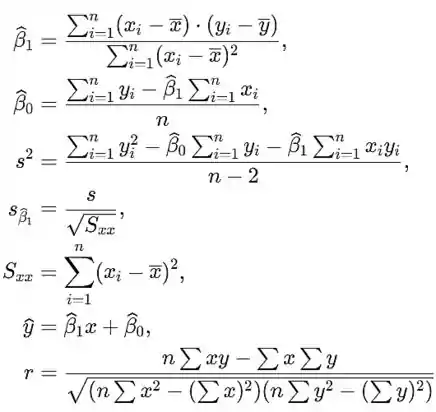
E o teste de utilidade do modelo é dado por:

H 0   : β 1 = 0   v s   H a   : β 1   ≠ 0

Com a estatística t

t = β ^ 1 s _ β ^ 1

  1. Nesta subseção usaremos o teste de utilidade do modelo com nível 0.01 usando a abordagem da região de rejeição. Temos o seguinte:

    2. β ^ 0 = 0.365

    β ^ 1 = 0.967

    t = β ^ 1 s _ β ^ 1

    = 5.29

    t α , n - 2 = t 0.01,13 - 2

    = t 0.01,11

    = T I N V 0.01 2 , 11

    = 3.1

    Como 5.29 é maior que 3.1 significa que rejeitamos hipóteses nulas e aceitamos a alternativa que β 1   ≠   0 . Assim, concluímos que esta variável tem influência no resultado para que o modelo seja bom.

    Passo 2

  2. Agora podemos ver na saída do MINITAB que o valor p para essa razão t para testar esse parâmetro β 1 é igual a zero é quase zero, então rejeitamos hipóteses nulas e aceitamos alternativas. Neste caso também concluímos que este modelo é bom para previsão.
  3. Agora supomos que N O 3 - aumenta em 0.1 g e do que precisamos examinar, N muda pelo menos 0.15%. Vamos examinar as próximas hipóteses

H 0   : β 1 = 0.015   v s   H 1   : β 1 < 0.015

Para este teste, usamos a próxima estatística de teste:

t = β 1 ^ - β 1 0 s β ^ 1

= 0.967 - 0.015 0.1829

= 5.27

t 0.01,13 - 2 = T I N V 0.01,11

= - 2.71

Como 5.27 é maior que -2.71 significa que aceitamos hipóteses nulas e rejeitamos alternativas. Assim, podemos concluir que essa mudança é de pelo menos 0.15 %

Resposta

Ver o desenvolvimento.

Exercícios de Livros Relacionados

Considere a situação do Exercício 11.30, massuponha n = 2 (ou seja, somente dois pontos dos dados estão disponíveis). Dê um argumento de que areta de regressão de mínimos quadrados resultará em(? 1~ S
Suponha que um cientista postule o modelo Y i = α + β x i + ϵ i ,i = 1,2 , … , n , e α é um valor conhecido, náo necessariamente 0 .(a) Qual é o estimador de mínimos quadrados de β ? Justifique.(b) Qu
Usando o valor de s2 encontrado no Exercício11.19(a), construa um intervalo de confiança de 95%para a quantidade de açúcar convertido que correspondea x = 1,6 no Exercício 11.3.11.28 Em relação ao Exe
Mostre os passos necessários ao converter a equaçâo r = b s / S m para a forma equivalente t = r n - 2 1 - r 2 .
Mostre que, no caso de um ajuste por mínimos quadrados do modelo de regressáo linear simples, Y i = α + β x i + ϵ i ,i = 1,2 , … , n ,∑ i = 1 n     y i - y ˆ i = ∑ i = 1 n     e i = 0 .