Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 30

Reconsidere a situação descrita no Exercício 7, no qual x resistência acelerada do concreto e y resistência ao tratamento de 28 dias. Suponha que o modelo de regressão linear simples seja válido para x entre 1000 e 4000 e que 1 1,25 e 350. Suponha um experimento no qual n 7 e os valores x, nos quais as observações são feitas, são x1 1000, x2 1500, x3 2000, x4 2500, x5 3000, x6 3500 e x7 4000. a. Calcule ˆ 1 , o desvio padrão deˆ 1. b. Qual é a probabilidade de o coeficiente angular estimado baseado nessas observações ficar entre 1,00 e 1,50? c. Suponha que também seja possível fazer uma única observação em cada um dos n 11 valores x1 2000, x2 2100, ... , x11 3000. Se o objetivo principal for estimar 1 com o máximo de precisão possível, o experimento com n 11 seria preferível ao experimento com n 7?

Passo 1

  1. A variância e o desvio padrão do estimador β ^ 1 são

    2. V β ^ 1 = σ 2 S x x

    σ β ^ 1 = σ S x x

    Onde S x x é

    S x x = ∑ x i 2 - 1 n ∑ x i 2

    Ao estimar o desvio padrão σ com s você obtém estimativa de σ β ^ 1

    s β ^ 1 = s S x x

    Usando o dado x 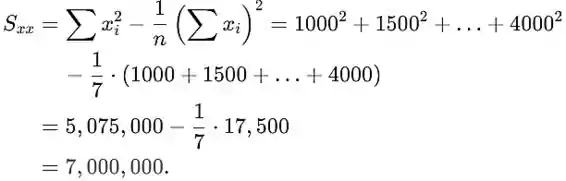i ' s , S x x é

    O valor de σ é conhecido e é σ = 350 ; assim, a variância do estimador é

    V β ^ 1 = σ 2 S x x = 350 7000000 0.0175

    e o desvio padrão do estimador β ^ 1 é

    Passo 2

  2. A probabilidade pode ser calculada padronizando a variável aleatória β ^ 1 .

    3. A média de β ^ 1 é

    E β ^ 1 = β 1

    portanto, β ^ 1 é um estimador imparcial do parâmetro β 1 .

    A média de β ^ 1 é

    E β ^ 1 = β 1 = 1.25

    que é dado no exercício.

    O desvio padrão foi calculado em (a); assim, vale o seguinte

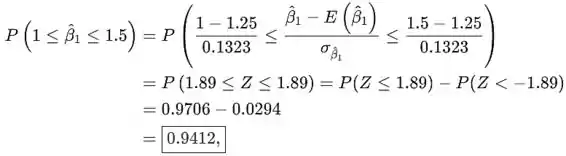
    onde as probabilidades exigidas podem ser encontradas no apêndice do livro ou computadas por um software.

    Passo 3

O objetivo é ver como a variância se comportará quando n=11 comparado a n=7; a variância menor é melhor.

Ao olhar na fórmula do denominador da variância, S x x , observe que se S x x for menor, a variância será maior - basicamente, o problema agora é calcular novos S x x e veja se é menor que o calculado em (a)(a). Usando o novo x i ' , S x x   é

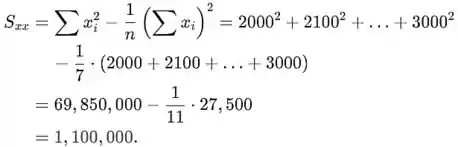
A conclusão: a variância é maior quando n=11 em comparação com o caso quando n=7, o que indica que o primeiro experimento (um em (a)) é preferível.

Resposta

  1. σ β ^ 1 = 0.1323
  2. 1   ≤   β ^ 1 ≤ 1.5 = 0.9412
  3. Não, experimente quando n=7 for preferível.

Exercícios de Livros Relacionados

Em relação ao Exercício 11.7, construa(a) um intervalo de confiança de 95% para a média dasvendas semanais quando são gastos $ 45 em publicidade;(b) um intervalo de predição de 95% para a venda semana
Mostre que, em um conjunto de dados de regressão linear múltipla, ∑ i = 1 n   h i = p
Um engenheiro de uma indústria de semicondutores deseja modelar a relação entre o ganho de um equipamento ou hFE (y) e três parâmetros: emissor-RS C^),base-RS ( x ,) e emissor para a base-RS (a\ ). O
Um conjunto de experimentos foi realizado paradeterminar uma maneira de prever o tempo de cozimento y em junção de vários níveis da largura do forno *, eda temperatura do gás * ,. Os dados codificados
Para o Exercício 12.8, construa um intervalo de confiança de 90% para a força compressiva média quando aconcentração éx = \9,5 e é usado um modelo quadrático.