Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 28
a. Considere os dados do Exercício 20. Suponha que, em vez de a reta dos mínimos quadrados passar pelos pontos (x1, y1), ..., (xn, yn), queiramos que ela passe por (x1 x , y1), ..., (xn x , yn). Elabore um gráfico de dispersão dos pontos (xi , yi ) e, em seguida, dos pontos (xi x , yi ). Use os gráficos para explicar intuitivamente como as duas retas dos mínimos quadrados estão relacionadas uma com a outra. b. Suponha que, em vez do modelo Yi 0 1xi i (i 1, . .., n), queiramos ajustar um modelo da forma Yi *0 *1(xi x) i (i 1, ..., n). Quais são os estimadores dos mínimos quadrados de *0 e *1 e como eles estão relacionados com ˆ 0 e ˆ 1?
Passo 1
- O gráfico de dispersão dos pontos de dados do exercício 20
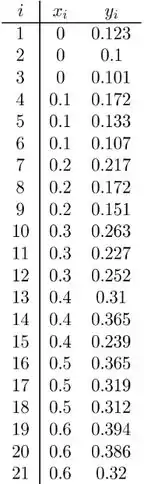
É dado abaixo
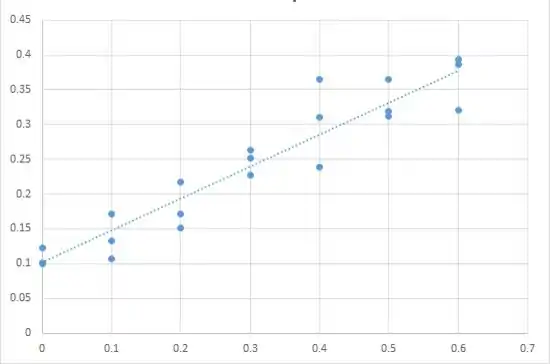
O gráfico de dispersão de pontos de dados do exercício 20 subtraído com o valor médio
É dado abaixo.
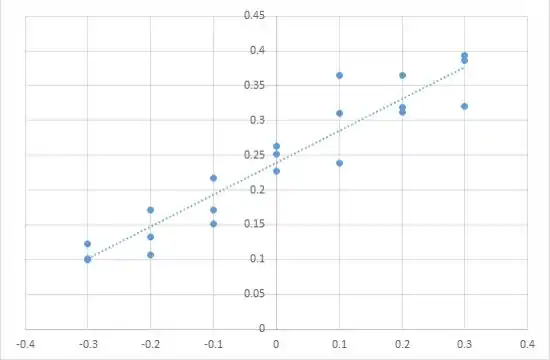
Dos gráficos de dispersão você pode notar que subtraindo de s apenas desloca os pontos para a esquerda em 0.3 unidades (ou geralmente por unidades). A forma da linha de regressão é a mesma - a inclinação é a mesma em ambas as linhas de regressão do gráfico de dispersão. Além disso, você pode notar que a interceptação da nova linha de regressão y é
Passo 2
Para obter o estimador de mínimos quadrados de e do modelo fornecido
Função
precisa ser minimizado, e o mínimo será a estimativa dos mínimos quadrados.
Usando cálculo, a partir do sistema de equações
as estimativas serão obtidas. Tomando as derivadas parciais, o sistema torna-se
que é igual a
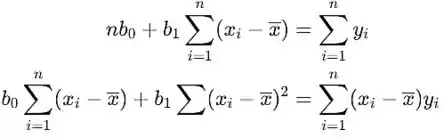
Passo 2
Do fato de que
a estimativa é, da primeira equação
Usando
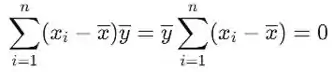
a estimativa de , da segunda equação, a igualdade mencionada, e o fato de torna-se
que é a mesma estimativa que a estimativa do modelo clássico
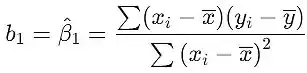
Assim, os estimadores são, para o intercepto
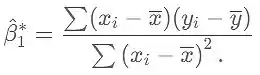
Resposta
Ver o desenvolvimento