Enunciado
Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 4.Problemas - Ex. 1
Sabe-se que uma determinada moeda apresenta cara três vezes mais frequentemente que coroa. Essa moeda é jogada três vezes. Seja o número de caras que aparece. Estabeleça a distribuição de probabilidade de e também a fd. Faça um esboço do gráfico de ambas.
Passo 1
Vamos lançar uma moeda 3 vezes. A probabilidade de sair cara em um lançamento é e a de sair coroa é . Sabemos isso pois o enunciado disse que sai cara com uma frequência três vezes maior do que sai coroa...
Trata-se de um claro exemplo de distribuição binomial com e . A distribuição de probabilidades para que saiam caras e coroas é:
Logo,
PS: a distribuição binomial sempre aparece quanto temos um evento binário (que pode dar sucesso ou fracasso) que se repete algumas vezes. A distribuição dá a probabilidade de haver sucessos em tentativas.
Passo 2
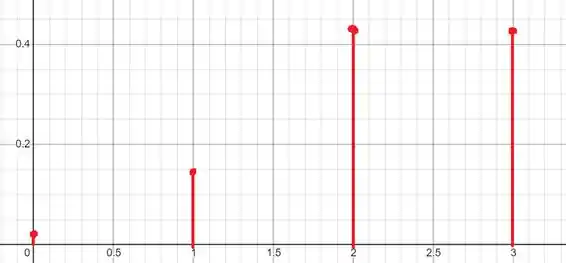
Para que não haja nenhuma cara ():
Para haver exatamente uma cara ():
Já para duas caras ():
Por fim, para :
Com isso, achamos a seguinte distribuição:
A seguir faço um esboço dessa distribuição discreta:
Passo 3
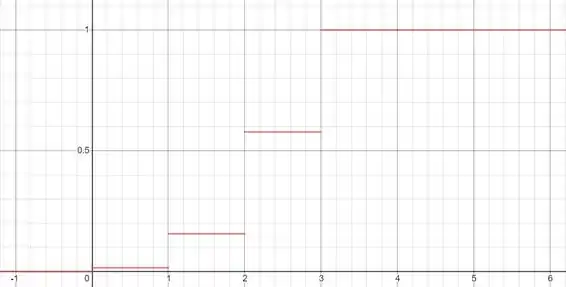
O exercício também pediu para acharmos a função distribuição acumulada . Para isso, basta somar todas as probabilidades correspondentes a valores menores que .
A ideia é assim: a função começa sendo zero. Aí, conforme vamos crescendo na variável , sempre que passamos por um ponto que tem alguma probabilidade, a função sofre um salto dessa probabilidade.
Para , temos que . Daí, quando passamos por a função salta para
Esse valor permanece até chegarmos em , quando ela salta para
Daí, quando passamos por ela salta para
E por fim, quando passamos por ela salta para
Com isso, a fd fica:
A seguir temos o gráfico dessa função:
