Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.5 - Ex. 2
Para verificar o efeito da variável X sobre a variável Y, foi realizado um experimento que forneceu os pares dados por Obtenha a reta ajustada. Construa o diagrama de dispersão baseando-se nos pares fornecidos e, em seguida, desenhe a reta ajustada. Baseando-se apenas no gráfico, você diria que o ajuste é adequado?
Passo 1
Fala ai meu querido, vamos resolver essa questão de Regressão Linear Simples. Acho que olhando de cara os pares fornecidos pelo exercício podemos observar que existe uma tendência de valores mais altos de X estarem associado a valores mais altos de Y, e valores mais baixos de X associados a valores mais baixos de Y, vamos confirmar isso com nosso estudo da questão.
Passo 2
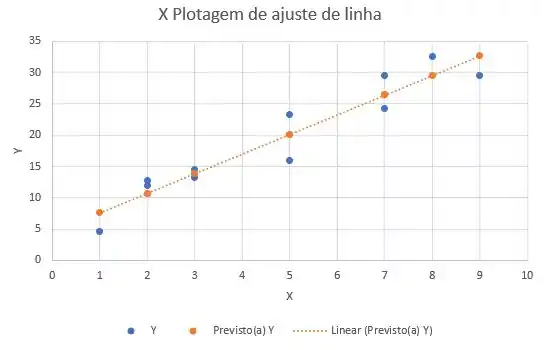
Utilizando uma planilha do Excel, montei uma regressão linear com ajuda da ferramenta “Análise de Dados”, e nosso gráfico ficou com a seguinte cara:
Passo 3
Confirmando nossas suspeitas, podemos observar pelo gráfico que o ajuste que fizemos para nosso problema parece ser adequado para as variáveis x e y. Nesse problema encontramos a seguinte equação:
Resposta
Ei, a resposta está no passo a passo :)