Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 6.Problemas - Ex. 12
Seja X com distribuição dada abaixo; calcule E(X). Considere a v.a. (X – a)² e calcule E(X – a)² para a = 0, 1/4, 1/2, 3/4, 1. Obtenha o gráfico de E(X – a)² = g(a). Para qual valor de a, g(a) é mínimo?
Passo 1
Passo 2
Substituindo os valores de a na equação (3), temos:
Passo 3
Os resultados encontram-se representados no gráfico a seguir, em que se percebe que g(a) é mínimo para a = 0,75.
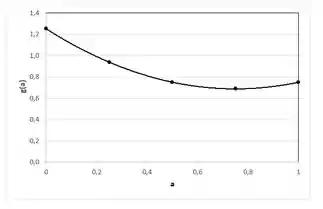
Resposta
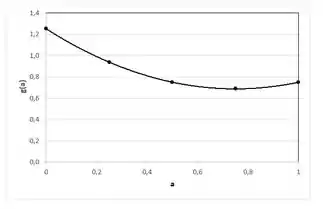
g(a) é mínimo para a = 0,75.
Exercícios de Livros Relacionados
Numa classe tem-se 7 homens e 3 mulheres. Sorteando-se 3 alunos, ao acaso e sem reposição, qual a média e o desvio padrão do número de homens sorteados?
Para qualquer valor de p1 , seja c p = ∑ x = 1 ∞ 1 x p . Suponha que X é uma variável aleatória discreta com a seguinte distribuição de probabilidade: f x = 1 c p x p ,x = 1,2 , … ( a ) para qualquer
Se a função de distribuição F da variável aleatória X fosse definida de uma das formas abaixo, descreva como as condições a ,be (c) do lema 2.4 . 1 deveriam ser modificadas em cada caso: i )F x = P xx
Seja X uma variável aleatória cuja função geradora de momentos é ϕ 1 : seja Y = a X + b , onde aeb são constantes reais e, por fim seja ϕ 2 a função geradora de momentos de Y . Então, para todo valor
Um pote contém m + n pedras, numeradas 1, 2, ..., n + m. Um conjunto de tamanho n é retirado do pote. Se X representar o número retirado de pedras cujo número é maior do que cada um dos números das pe