Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 4.4 - Ex. 10b

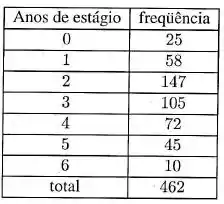
O Sindicato dos Engenheiros do Estado de São Paulo está estudando o impacto do estágio na obtenção de bons empregos. Dentre os engenheiros recém-formados e com empregos considerados bons, foi sorteada uma amostra e observado o número de anos de estágio anteriores à formatura, conforme a tabela a seguir.

Para efeito de análise, decidiu-se desprezar os valores que se distanciassem da média amostral por mais de dois desvios-padrão, isto é, só serão considerados os valores no intervalo x o b s ± 2 d p o b s . Recalcule o item   ( a )   e comente os resultados.

Passo 1

A média, que calculamos no item ( a ) é igual a 2,62 . E o desvio padrão será d p = 1,95 = 1,4 .

Agora, só consideraremos então os valores que 2,62 ± 2 × 1,4 , ou seja, 2,62 ± 2,8 . Portanto, na nova tabela só terão valores entre 0 e 5,42 .

Assim, só não será considerado 6 anos de estágio.

Passo 2

Calculando a nova média, temos:

x - = 1 n × ∑ i = 1 k n i × x i

= 25 + 58 + 147 × 2 + 105 × 3 + 72 × 4 + 45 × 5 462 = 1151 462 = 2,49 .

Passo 3

Calculando agora a variância, temos que:

v a r = 1 n × ∑ i = 1 k n i × x i - x - 2

= 0 - 2,62 2 × 25 + 1 - 2,62 2 × 58 + 147 × 2 - 2,62 2 + 105 × 3 - 2,62 2 + 72 × 4 - 2,62 2 + 45 × 5 - 2,62 2 462

= 171,6 + 152,2 + 56,5 + 15,2 + 137,1 + 254,9 462 = 787,5 462 = 1,70 .

Resposta

Assim, concluímos o que foi desejado.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ensaio de tração mede a qualidade de uma solda a ponto de um material revestido de alumínio. A fim de determinar se há um “efeito de máquina” quando se solda um material de bitola especificada, obt
Quatro analistas determinam o rendimento de dado processo. Por comodidade, oitenta unidades foram subtraídas dos dados originais a fim de dar a seguinte tabela de valores:Pede-se:Diferem os analistas
Uma máquina para ensaio de desgaste consta de quatro escovas carregadas, sob as quais se fixam amostras do material, a fim de medir suas resistências à abrasão. A perda de peso do material, depois de
Os dados da tabela seguinte referem-se à quantidade de um produto feita por dado método. Os quatro níveis do fator A representam postos de trabalho. Os dois níveis do fator B representam os supervisor
Admitindo-se que as notas em Estatística, para cada turma, distribuem-se normalmente com mesma variância, quer-se saber se as médias obtidas nas provas de aproveitamento em cada uma das turmas são igu