Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 10b
Suponha que e tenham a seguinte distribuição conjunta:
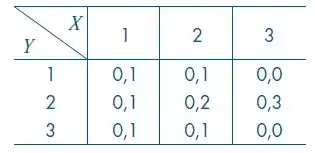
b) Determine a f.p. de e, em seguida, calcule
Passo 1
Vamos encontrar a função de probabilidade de .
A distribuição para a probabilidade de está representada na tabela abaixo, onde representa a probabilidade de ocorrência do evento.
Vamos, agora, calcular .
Sabemos que:
Assim, com base na tabela de probabilidades representada acima, basta calcularmos o produto dos termos de cada coluna e efetuarmos o somatório dos resultantes:
Resposta
Portanto,
E a tabela que representa a função de probabilidade de é:
Exercícios de Livros Relacionados
Numa sala estão cinco crianças cujas idades são (em anos): 3, 3, 4, 5, 5. Escolhem-se três crianças ao acaso para formar uma trinca. X indica a idade da mais nova da turma, e Y à da mais velha. Calcul
(a) No Problema 3, calcule E ( X + Y )eV a r ( X + Y ) . (b) Se Z=a X + b Y , calcule a e b de modo que E ( Z ) = 10 e V a r Z =600 .
No Problema 2, obtenha as distribuições de X + Y e de X Y . Calcule E ( X + Y ) ,E ( X Y ) ,V a r ( X + Y ) ,V a r ( X Y ) .
Dois tetraedros (dados com quatro faces) com as faces numeradas de um a quatro são lançados e os números das faces voltadas para baixo são anotados. Sejam as v.a.:X: maior dos números observados; Y: m
(d) Como seriam as respostas anteriores se a primeira tira de papel não fosse devolvida à urna antes da segunda extração?