Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 4

No Problema 2, obtenha as distribuições de X + Y e de X Y . Calcule E ( X + Y ) ,   E ( X Y ) ,   V a r ( X + Y ) ,   V a r ( X Y ) .

Passo 1

Vamos relembrar a Tabela do Problema 2, que dá a distribuição conjunta das variáveis aleatórias X e Y?

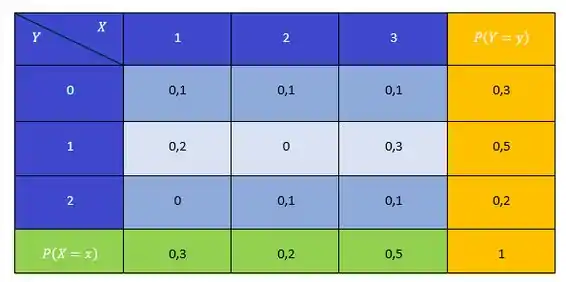
A partir dela, podemos achar a v.a. X + Y, e a v.a. XY. A soma X + Y é definida naturalmente: a cada resultado do experimento, ela associa a soma dos valores de X e Y, isto é,

X + Y ω = X ω + Y ( ω )

Do mesmo modo,

X Y ω = X ω Y ( ω )

Podemos, então, construir uma tabela com os valores de X + Y e de X Y .

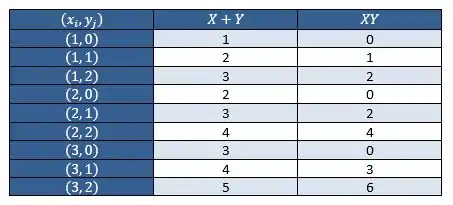
Passo 2

Estão faltando as probabilidades, né?

Vamos calculá-las e montar as nossas tabelas das distribuições de X + Y e de X Y ?

P X + Y = 1 = P X = 1 , Y = 0 = 0,1

P X + Y = 2 = P X = 1 ,   Y = 1 + P X = 2 , Y = 0 = 0,2 + 0,1 = 0,3

P X + Y = 3 = P X = 1 , Y = 2 + P X = 2 , Y = 1 + P X = 3 , Y = 0 = 0,1

P ( X + Y = 4 ) = P X = 2 , Y = 2 + P X = 3 , Y = 1 = 0,1 + 0,3 = 0,4

P X + Y = 5 = P X = 3 , Y = 2 = 0,1

P X Y = 0 = P X = 1 , Y = 0 + P X = 2 , Y = 0 + P X = 3 , Y = 0 = 0,1 + 0,1 + 0,1 =

        = 0 , 3

P X Y = 1 = P X = 1 , Y = 1 = 0,2

P X Y = 2 = P X = 1 , Y = 2 + P X = 2 , Y = 1 = 0 + 0 = 0

P X Y = 3 = P X = 3 , Y = 1 = 0,3

P X Y = 4 = P X = 2 , Y = 2 = 0,1

P X Y = 6 = P X = 3 , Y = 2 = 0,1

Construindo as nossas tabelas, temos

Passo 3

Agora, com base nas tabelas das distribuições de X+Y e de XY, vamos calcular E X + Y ,   E X Y ,   V a r X + Y ,   V a r X Y .

E X + Y = 1 0,1 + 2 0,3 + 3 0,1 + 4 0,4 + 5 0,1 = 3,1

E X + Y 2 = 1 2 0,1 + 2 2 0,3 + 3 2 0,1 + 4 2 0,4 + 5 2 0,1 = 11,1

Portanto

V a r X + Y = E X + Y 2 - E X + Y 2 = 11,1 - 3,1 2 = 1,49

De modo análogo

E X Y = 0 0 , 3 + 1 0 , 2 + 2 0 + 3 0 , 3 + 4 0 , 1 + ( 6 ) ( 0,1 ) = 2 , 1

E X Y 2 = 0 2 0,3 + 1 2 0,2 + 2 2 0 + 3 2 0,3 + 4 2 0,1 + 6 2 ( 0,1 ) = 8 , 1

Portanto

V a r X + Y = E X + Y 2 - E X + Y 2 = 8,1 - 2 , 1 2 = 3,6 9

Resposta

E X + Y = 3,1                               V a r X + Y = 1,49                               E X Y = 2,1                               V a r X Y = 3,69

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere que os pesos de indivíduos sejam independentes e normalmente distribuídos, com uma média de 160 libras e um desvio padrão de 30 libras. Suponha que 25 pessoas se espremam em um elevador proj
A espessura de um filme fotorresistente usado na fabricação de semicondutores tem uma média de 10 micrômetros e um desvio padrão de 1 micrômetro. Considere que a espessura seja normalmente distribuída
A confecção de postos de cerâmicas é feito em duas etapas: elaboração do pote em torno do oleiro e o cozimento. O tempo de giro do torno Do torno e do cozimento são variáveis aleatórias normalmente di
Um artigo em Knee Surgery Sports Traumatology Arthroscopy “Effect of provider volume on resource utilization for surgical procedures” -Efeitos do volume de cirurgias na utilização de recurso para proc
Latas de refrigerante são cheias porque é uma máquina de enchimento automático, sendo o desvio padrão = 0.5 onças fluídas. Considere que o volume de enchimentos 10 latas sejam variáveis aleatórias nor