Ajustar uma curva normal às distribuições amostrais a seguir:

Passo 1
Olá galerinha, vamos resolver mais um exercício juntos? Então vamos lá!
Muitas vezes poderemos estar interessados em saber se uma determinada distribuição amostral segue um determinado modelo de distribuição teórica, tais como, a distribuição normal, binomial e Poisson. Dessa forma, levando em consideração se a distribuição amostral possui variável discreta ou contínua, se é um evento dicotômico ou raro, escolhemos a distribuição teórica que queremos ajustar.
Como nosso enunciado tem a nossa distribuição amostral, conseguimos calcular (média da amostra) e (desvio padrão da amostra), pelas seguintes equações:
Onde:
- mediana ();
- ;
- ;
- valores que iremos estimar para .
Sendo assim, temos os seguintes dados:

Então:
Passo 2
Agora precisamos calcular o valor de :
Com os valores de e com a tabela de distribuição normal padrão, conseguimos encontrar o valor de . Sendo assim, temos os seguintes dados:
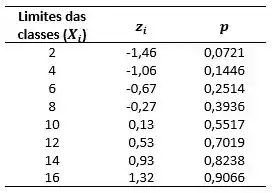
Dando o exemplo, de como encontramos os valores de , para , temos:
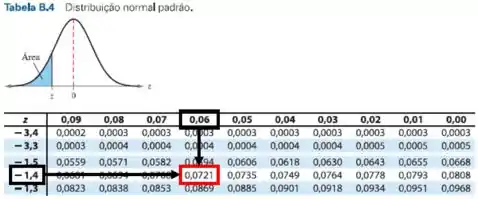
Isso foi realizado para cada valor de .
Passo 3
Para descobrirmos a probabilidade das classes, iremos subtrair os valores de . Por exemplo, para a classe de 2 ⱶ- 4:
Fazendo para cada limite da classe obtemos:

Finalmente conseguimos encontrar a frequência esperada ():
Então obtemos o seguinte:

Tchau galerinha! Te espero em mais exercícios.
Resposta
Resposta no Passo 3.