Determinar os valores de , para a distribuição de Student, que satisfaçam cada uma das seguintes condições:
- área entre e de 90%, com ;
- área à esquerda de de 2,5%, com ;
- soma das áreas à direita de e à esquerda de de 1%, com ;
- área à direita de de 55%, com .
Passo 1
Oi pessoal. Vamos pensar juntos neste exercício?!
A variável não é normal, e sua distribuição é conhecida como distribuição de Student, com graus de liberdade (). A maneira mais comum de tabelamento é na qual, para cada valor de e , a tabela fornece um valor .
Então vamos lá para o nosso exercício. Do item a), temos que:
E queremos descobrir o valor de para a área entre e com . Então pela tabela de distribuição :
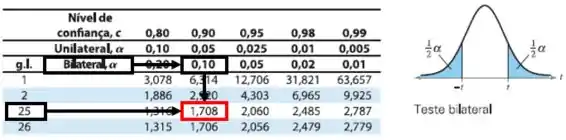
Então:
Passo 2
No item b), temos:
E queremos descobrir o valor de para a área à esquerda de com . Então pela tabela de distribuição :
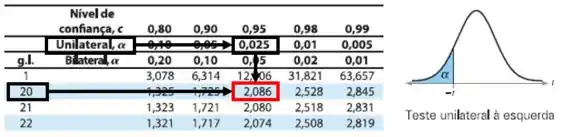
Então:
Passo 3
Para o item c) temos:
Neste item, queremos descobrir o valor de para a soma à direita de e à esquerda de com . Então pela tabela de distribuição :
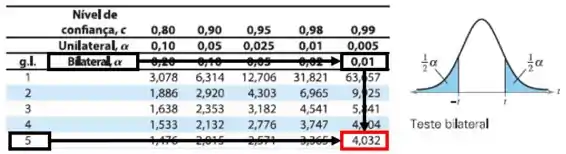
Então:
Passo 4
E por fim, para o item d), temos:
E queremos descobrir o valor de para a área à direita de com . Como na nossa tabela não temos o valor para , iremos usar o comando “INV.T” do programa Excel, da seguinte maneira:
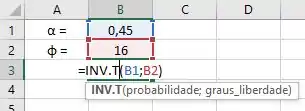
Obtendo o seguinte resultado:
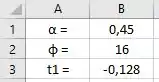
Então:
Prontinho pessoal. Até mais!
Resposta
- ;
- ;
- ;
- .