Comparar os resultados de uma distribuição Binomial com e , com uma distribuição normal com mesma média () e mesma variância (). Verificar que a aproximação é bem razoável para valores próximos da média.
Obs.: a) efetuar correção de continuidade;
b) trabalhar com 4 casas decimais;
c) lembrar que a distribuição normal é simétrica.
Passo 1
Olá galerinha, vamos resolver mais um exercício juntos? Então vamos lá!
Como a distribuição Binomial é caracterizada para uma variável discreta, enquanto que a Normal é para uma variável contínua, devemos efetuar a correção de continuidade. Tal correção consiste em considerar que a probabilidade de ocorrer um valor genérico na distribuição Binomial. Sendo assim, iremos calcular a probabilidade de ocorrer um valor entre e na distribuição Normal.
Neste exercício iremos utilizar a distribuição normal e binomial, e pelo enunciado sabemos que:
- ;
- ;
Para a distribuição normal, precisamos fazer o cálculo da média () e do desvio padrão ():
Passo 2
Iremos encontrar os valores da distribuição Normal, pela seguinte equação:
Para :
Pela Tabela da distribuição Normal, temos:
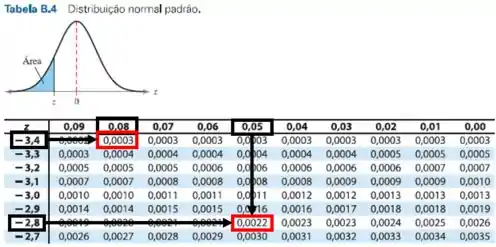
Passo 3
Para o cálculo pela Binomial, utilizamos a equação:
Fazendo o mesmo para , obtemos os resultados:
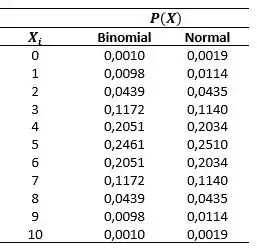
Tchau galerinha! Te espero em mais exercícios.
Resposta
A aproximação é razoável, principalmente para valores próximos da média.