Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 40b

As tabelas a seguir contêm o número de pessoas segundo origem e opinião a respeito do aborto.

  1. Combine as informações em uma única tabela desconsiderando sexo e teste novamente a independência das variáveis.
  2. Discuta os resultados obtidos em (a) e (b)

Passo 1

Antes de mais nada perceba que na alternativa B também temos um teste de independência; então relembrando:

X = O r i g e m   d o s   p a r t i c i p a n t e s .

E

Y = o p i n i ã o   a   r e s p e i t o   d o   A b o r t o .

Para as seguintes hipóteses:

H 0 : X   e   Y   s ã o   i n d e p e n d e n t e s         c o n t r a           H 1 : X   e   Y   s ã o   d e p e n d e n t e s

Dando uma recordada em como fazemos isso:

Q 2 = ∑ i = 1 t ∑ j = 1 s o i , j - E i , j 2 E i , j ~ X t - 1 s - 1 2

Onde t   e s representam as linhas e colunas respectivamente com t - 1 ( s - 1 ) graus de liberdade e o i , j é exatamente o valor DADO em cada célula; ou seja, os valores presentes na tabela do enunciado.

Já o E i , j representa um valor ESPERADO para cada célula, ou seja:

E 1,1 = T o t a l   l i n h a   1 T o t a l   c o l u n a   1 T o t a l   G e r a l

E 1,2 = T o t a l   l i n h a   1 T o t a l   c o l u n a   2 T o t a l   G e r a l

E assim por diante, fazendo um arranjo das linhas e colunas.

Passo 2

Beleza, agora a única diferença da letra B é que devemos “fundir” a tabela ignorando os sexos; portanto teremos uma nova tabela tipo assim:

Bem deboas né?! O processo agora é exatamente igual feito anteriormente. Bora lá então:

E 1,1 = 65 + 85 65 + 40 65 + 85 + 40 + 110 = 150 105 300 ≅ 52,50

E assim por diante até:

E 2,2 = 150 195 300 ≅ 97,50

E aí chegamos numa nova tabelinha só com esses valores encontrados:

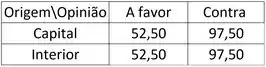
Tranquilis? A região crítica, é a mesma da alternativa A; tomando α = 5 % :

R C = q o b s ∈ R   q o b s ≥ q 0,05 }  

Portanto devemos buscar:

P X 0,05 2 ≥ q 0,05 = 0,05 = α

Na tabela de distribuição qui-quadrado, na coluna de 5% e na linha de de 2 - 1 2 - 1 = 1 grau de liberdade:

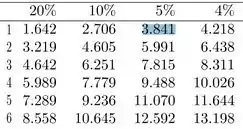
Chegamos em:

R C = q o b s ≥ 3,841

Passo 3

Agora, só resta a nós obter:

q o b s = 65 - 52,50 2 52,50 + 85 - 97,50 2 97,50 + 40 - 52,50 2 52,50 + 110 - 97,50 2 97,50 ≅ 9,157

Portanto, q 0 b s = 9,157 ∈ R C ; então devemos rejeitar a hipótese nula.

Note que, quando havia distinção com base no sexo da amostra as variáveis eram independentes; ao excluirmos o sexo dos participantes, as variáveis se tornaram dependentes.

Resposta

Ao desconsiderarmos o sexo, encontramos evidências de que a opinião a respeito do aborto depende da origem da pessoa.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma amostra de 5 0 parafusos produzidos por uma máquina forneceu a distribuição de frequência abaixo. Ajustar uma distribuição normal e efetuar o teste de aderência, com α = 0,02 .
Uma urna contém um grande número de bolas brancas, pretas, azuis, amarelas, verdes e vermelhas. Foram retiradas 100 bolas ao acaso e encontramos 36 brancos, 21 pretas, 7 azuis, 12 amarelas, 10 verdes
Três moedas desconhecidas foram lançadas 200 vezes, anotando-se o número de coroas surgidas em cada lançamento. Para α = 0,05 , testar a hipótese de que as moedas são honestas ajustando uma binomial.
A enfermaria de uma faculdade conduziu um experimento para determinar o grau de alívio fornecido por três remédios antitussígenos. Cada remédio foi testado em 50 estudantes e os seguintes dados foram
Uma amostra aleatória de 200 homens casados, todos aposentados, foi classificada de acordo com o nível educacional e o número de filhosTeste a hipótese de que, num nível de significância de 0,05 , o t