Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 40a

As tabelas a seguir contêm o número de pessoas segundo origem e opinião a respeito do aborto.

  1. Para cada sexo, verifique se origem e opinião são independentes.
  2. Combine as informações em uma única tabela desconsiderando sexo e teste novamente a independência das variáveis.
  3. Discuta os resultados obtidos em (a) e (b)

Passo 1

E aí confrade, essa vai ser longa em... bora lá

Perceba que temos duas variáveis sendo estudadas em duas subpopulações, esse exercício basicamente juntou tudo p que vinhamos fazendo até agora; temos o seguinte:

X = O r i g e m   d o s   p a r t i c i p a n t e s .

E

Y = o p i n i ã o   a   r e s p e i t o   d o   A b o r t o .

Na letra A iremos realizar primeiro o teste de independência para essas duas variáveis; você lembra o processo? É mais ou menos assim:

Considerando as seguintes hipóteses:

H 0 : X   e   Y   s ã o   i n d e p e n d e n t e s         c o n t r a           H 1 : X   e   Y   s ã o   d e p e n d e n t e s

Realizamos o teste aproximado pela distribuição Qui-quadrado:

Q 2 = ∑ i = 1 t ∑ j = 1 s o i , j - E i , j 2 E i , j ~ X t - 1 s - 1 2

Onde t   e s representam as linhas e colunas respectivamente com t - 1 ( s - 1 ) graus de liberdade e o i , j é exatamente o valor DADO em cada célula; ou seja, os valores presentes na tabela do enunciado.

Já o E i , j representa um valor ESPERADO para cada célula, ou seja:

E 1,1 = T o t a l   l i n h a   1 T o t a l   c o l u n a   1 T o t a l   G e r a l

E 1,2 = T o t a l   l i n h a   1 T o t a l   c o l u n a   2 T o t a l   G e r a l

E assim por diante, fazendo um arranjo das linhas e colunas. Felizmente temos só duas linhas e duas colunas em cada tabela. Vamos calcular isso então:

Passo 2

  1. Para o sexo masculino:

    2. Vamos começar calculando os valores esperados:

    E 1,1 = 10 + 45 10 + 18 10 + 45 + 18 + 90 = 55 28 163 ≅ 9,45

    Bem tranquilinhi né? Fazendo isso até:

    E 2,2 = 108 135 163 ≅ 89,45

    E aí ficamos com os seguinte valores esperados em cada célula:

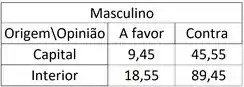
    Belezinha ? Agora como o enunciado não diz nada a respeito do nível de significância, vamos optar pelo padrão: α = 5 % .

    E então nossa região crítica será algo do tipo:

    R C = q o b s ∈ R   q o b s ≥ q 0,05 }  

    Precisamos então buscar na tabela de distribuição qui-quadrado um valor q 0,05 , tal que:

    P X 0,05 2 ≥ q 0,05 = 0,05 = α

    É bem tranquilo, basta irmos na coluna que representa 5% e na linha de 2 - 1 2 - 1 = 1 grau de liberdade; mais fácil impossível né?!

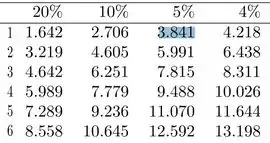
    Então: q 0,05 = 3,841 , portanto nossa RC assume a seguinte forma:

    R C = q o b s ≥ 3,841

    Agora só nos resta realizar o teste:

    q o b s = 10 - 9,45 2 9,45 + 45 - 45,55 2 45,55 + 18 - 18,55 2 18,55 + 90 - 89,45 2 89,45 ≅ 0,058

    Ou seja, q o b s = 0,058 não pertence à região crítica; portanto aceitamos a hipótese nula.

    Passo 3

  2. Para o sexo Feminino:

Mesmíssima idéia:

E 1,1 = 55 + 40 55 + 22 55 + 40 + 22 + 20 = 95 77 137 ≅ 53,39

Até:

E 2,2 = 42 60 137 ≅ 18,39

Chegamos no seguinte:

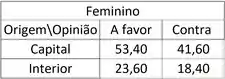
Nossa região crítica, será a mesma:

R C = q o b s ≥ 3,841

O que muda obviamente é o valor observado:

q o b s = 55 - 53,40 2 53,40 + 40 - 41,60 2 41,60 + 22 - 23,60 2 23,60 + 20 - 18,40 2 18,40 ≅ 0,357

Portanto, para o sexo feminino, q o b s também não pertence à região crítica. Também aceitamos H 0 .

Resposta

Concluimos que origem e opinião a respeito do aborto são independentes para ambos os sexos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na tabela abaixo, X significa número de filhos homens em famílias com 12 filhos. Calcule para cada valor da variável o número de famílias que você deveria esperar se X ~ b ( 12 ; 0,5 ) .Você acha que
Determinado tipo de parafuso é vendido em caixas com 1.000 peças. É uma característica da fabricação produzir 10% com defeito. Normalmente, cada caixa é vendida por $13,50. Um comprador faz a seguinte
Em um experimento para estudar a relação entre hipertensão e o hábito de fumar, os seguintes dados foram obtidos de 180 indivíduosTeste a hipótese de que a presença ou ausência da hipertensão depende
Uma amostra aleatória de 90 adultos é classificada de acordo com o gênero e o número de horas que eles assistem à televisão durante a semana:Use o nível de significância de 0,01 e teste a hipótese de
Um criminologista conduziu uma pesquisa para determinar se a incidência de certos tipos de crime varia de acordo com a região de uma cidade grande. Os tipos de crime de interesse são: agressão, arromb