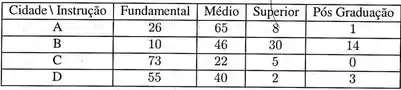
Deseja-se comparar o grau de instrução dos habitantes de quatro cidades brasileiras que têm aproximadamente o mesmo tamanho populacional. Uma amostra de 100 habitantes foi sorteada em cada cidade e o nível educacional das pessoas foi observado. Dos resultados apresentados na tabela abaixo, que conclusão podemos tirar, usando nível descritivo?

Vamos encontrar esses valores:

E assim por diante... Repare que como o tamanho da amostra em cada subpopulação é igual (100), os valores se repetirão 4 vezes, basta então calcular para a primeira linha e obteremos a mesma coisa para as linhas restantes.

E

Agora, vou colocar esses valores numa tabelinha:

Assim não dá pra errar né?! Pior que dá... repara uma coisinha, quando obtemos um valor esperado menor do que 5, devemos agrupar uma categoria. Tendeu nada né?

Peraí, veja só o que acontece na tabela abaixo:

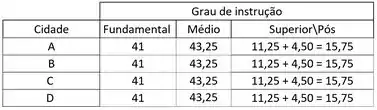
Reparou? Agrupamos uma categoria pois tínhamos encontrado um valor menor do que para ela.

E isso também ocorre na tabela original, a fusão das categorias “superior e pós”, com isso devemos somar os valores dessas duas categorias. Vou colocar mais uma tabela, mostrando como fica a original depois da fusão:

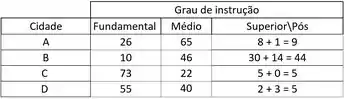
Finalmente podemos realizar o teste:

O exercício pede pra usar nível descritivo, então vamos relembrar que diaxo é isso; nada mais é do que a chance de termos um valor mais extremo ainda do que aquele ali que acabamos de achar.

Ou seja,

Cara, simplesmente tabela nenhuma vai ter esse valor, porque a chance de ter ele é muitíssima demais pequena, é quase 0.

Mas para dar uma resposta bonitinha, vamos responder assim:

É muito pequena mesmo, com isso por definição, quando o nível descritivo é pequeno devemos rejeitar a hipótese nula.