Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 6.Problemas - Ex. 26

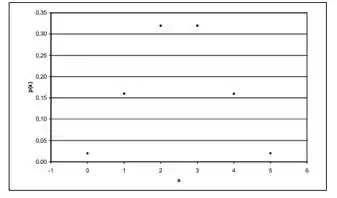
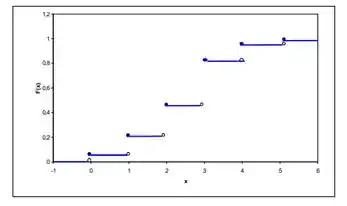
Se X tem distribuição binomial com parâmetros n = 5 e p = 1/2, faça os gráficos da distribuição de X e da f.d.a. F(x).

Passo 1

Lembrando da fórmula da Binomial

P X = k = n k   p k q n - k ,   k = 0 ,   1 ,   2 ,   … ,   n

E sabendo que

F x = P X ≤ x

Para fazermos os gráficos, basta calcularmos P X = 0 ,   P X = 1 , … , P X = 5   e   F X = 0 , F X = 1 , … F ( X = 5 ) .

Passo 2

X ~ b 5 ; 1 2

P X = 0 = 5 0   1 2 0 1 2 5 = 0,03125

P X = 1 = 5 1   1 2 1 1 2 4 = 0,15625

P X = 2 = 5 2   1 2 2 1 2 3 = 0,31250

P X = 3 = 5 3   1 2 3 1 2 2 = 0,31250

P X = 4 = 5 4   1 2 4 1 2 1 = 0,15625

P X = 5 = 5 5   1 2 5 1 2 0 = 0,03125

Agora calculando a f.d.a. de X...

F 0 = P X = 0 = 0,03125

F 1 = P X = 0 + P X = 1 = 0,18750

F 2 = P X = 0 + P X = 1 + P X = 2 = 0,5

F 3 = P X = 0 + … P X = 3 = 0,81250

F 4 = P X = 0 + … P X = 4 = 0,96875

F 5 = P X = 0 + … P X = 5 = 1

UFA!!! Agora basta plotarmos os gráficos.

Passo 3

O gráfico da distribuição de X, P(X=k) é:

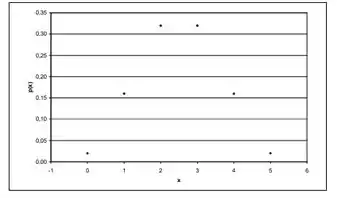
Passo 4

O gráfico da f.d.a de X, F(x) é:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sistema abaixo, cada componente tem probabilidade p de funcionar. Supondo independência de funcionamento dos componentes, qual a probabilidade de:(a) o sistema funcionar? (b) o sistema não funciona
Prove que
Prove a relação (6.19).
Se X ~ b ( n ,p ) , prove que E X = n p eV a r ( X ) = n p q . (Sugestão: calcule E ( X ) e V a r ( X ) para n=1 ,2 ,. . .e t c .)
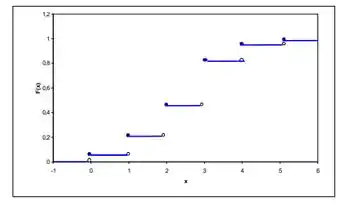
Discuta a validade do modelo Binomial nos seguintes casos:Dos alunos de uma grande universidade, sorteamos 5 e contamos quantos declaram usuários de droga.Escolhemos 20 lâmpadas ao acaso na prateleira