Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 6.Problemas - Ex. 51

No sistema abaixo, cada componente tem probabilidade p de funcionar. Supondo independência de funcionamento dos componentes, qual a probabilidade de:

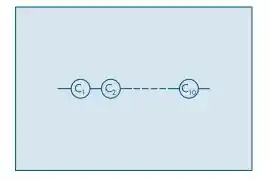
(a) o sistema funcionar?

(b) o sistema não funcionar?

(c) exatamente dois componentes funcionarem?

(d) pelo menos cinco componentes funcionarem?

Passo 1

Seja X o número de componentes que funcionam.Tem-se que X   ~ b   ( 10 ;   p ) .

Lembrando da fórmula da Binomial

P X = k = n k   p k ( 1 - p ) n - k ,   k = 0 ,   1 ,   2 ,   … ,   n

Agora vamos matar cada alternativa.

Passo 2

(a) Qual a probabilidade de o sistema funcionar?

Para o sistema funcionar, todos os componentes precisam funcionar, isto quer dizer X = 10 . Portanto

P f u n c i o n a r = P X = 10 = p 10

Passo 3

(b) Qual a probabilidade de o sistema não funcionar?

Nessa alternativa, podemos lembrar daquela ideia do complementar, portanto se a probabilidade do sistema funcionar é p 10 , do sistema não funcionar é 1 - p 10 .

Matematicamente...

P n ã o   f u n c i o n a r = P X < 10 = 1 - p 10

Passo 4

(c) Qual a probabilidade de exatamente dois componentes funcionarem?

Exatamente dois componentes funcionares significa que X = 2 , portanto

P X = 2 = 10 2 ×   p 2 × 1 - p 8 = 45 × p 2 × 1 - p 8

Passo 5

(d) Qual a probabilidade de pelo menos cinco componentes funcionarem?

Pelo menos cinco componentes funcionarem significa que X ≥ 5 , portanto

P X ≥ 5 = ∑ k = 1 5 10 k ×   p k × 1 - p 10 - k

Resposta

(a) P X = 10 = p 10

(b) P X < 10 = 1 - p 10

(c) p X = 2 = 45 × p 2 × 1 - p 8

(d) P X ≥ 5 = ∑ k = 1 5 10 k ×   p k × 1 - p 10 - k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma moeda, cuja probabilidade de cara em um lançamento é p ,0p1 , é lançada indefinidamente até que ocorra uma sequência de cinco caras (seguidas). Um estudante resolve modelar esse experimento defini
Sabe-se que a porcentagem de vitórias para que o time de basquete da NBA Chicago Bulls fosse para as finais das temporadas de 1996-97 era de 87,7. Arredonde-a para 90 para usar a Tabela A. 1.(a) Qual
No Exercício 5-9, quantos dos 15 caminhões vocês esperaria que tivessem pneus furados? De acordo com o teorema de Chebyshev, há uma probabilidade de pelo menos 3/4 de que o número de caminhões com pne
Um engenheiro de controle de tráfego relata que 75% dos veículos que passam por um ponto de checagem são do estado. Qual é a probabilidade de que menos de quatro dos próximos nove veículos sejam de fo
Sabe-se que 60% dos camundongos inoculados com soro estão protegidos contra determinada doença. Se cinco camundongos são inoculados, determine a probabilidade de que(a) nenhum contraia a doença;(b) me